强大数定律与弱大数定律

最近学习的时候遇到了强大数定律与弱大数定律，两者的区分提到了“依概率收敛”和“几乎处处收敛”，由于本人的数学基础太差，一直很难理解这个地方，在网上查阅了一些资料有了一些个人的理解，不知道对不对，不过还是想记录下来。提前说明，这里给出的解释非常的不严格，甚至有点搞笑，不过个人觉得很容易理解。

首先给出来强弱大数定律的表述。

对于独立同分布的无穷随机序列 \(\{X_i\}\)，期望为 \(\mathbb{E}(X_i)=\mu\)。大数定律要研究的就是样本均值的极限 \[ \bar{X}_n=\frac{1}{n}(X_1+\cdots+X_n) \\ \bar{X}_n\to \mu \quad\text{ for }\quad n\to \infty \] 他们的主要不同点在于收敛性的强弱不同。

弱大数定律：样本均值依概率收敛(converges in probability)于期望 \[ \lim_{n\to\infty}\text{Pr}\left(\vert \bar{X}_n-\mu \vert > \varepsilon\right)=0 \] 强大数定律：样本均值几乎处处收敛(converges almost surely)于期望 \[ \text{Pr}(\lim_{n\to\infty}\vert \bar{X}_n-\mu \vert > \varepsilon)=0 \\ \iff \text{Pr}(\lim_{n\to\infty} \bar{X}_n =\mu )=1 \]

从形式上来看似乎只是把极限和概率交换了一下位置，但是这个交换就导致了本质的区别，后面会解释。这里首先参考强大数定律和弱大数定律的本质区别？ - runze Zheng的回答 - 知乎，这个回答以及网上很多的解释主要是从“依概率收敛”与“几乎处处收敛”的角度出发，我觉得这个对理解很有帮助。下面简单复述这篇回答。

注：这部分内容摘自知乎回答

1. 依概率收敛的例子

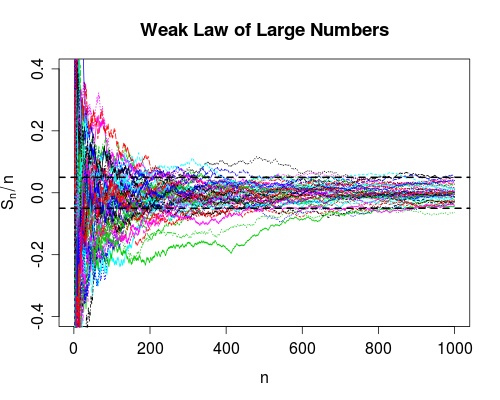
考虑下图，图中的每条线都代表一个数列，虚线表示一个非常小的区间。总的来说每个数列都越来越趋近0，且大部分时候不会超过虚线所表示的小边界，但是，偶尔会有一两条线超过虚线、然后再回到虚线之内。而且我们不能保证，有没有哪一个数列会在未来再次超出虚线的范围然后再回来——虽然概率很小。注意虚线的范围可以是任意小的实数，此图中大约是\(\pm 0.04\)，可以把这个边界缩小到\(\pm 0.004\)，甚至\(\pm 4*10^{-10}\)，随你喜欢，这个性质始终存在。

2. 几乎处处收敛的例子

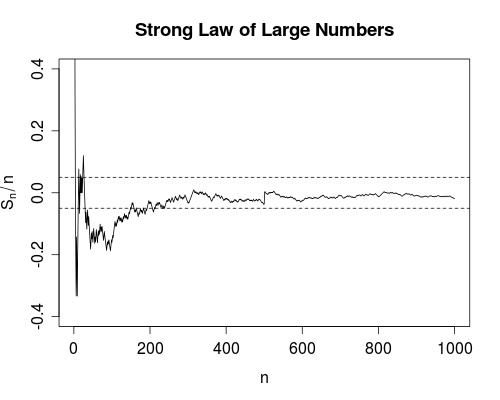
图中的黑线表示一个随机数列，这个数列在大约 \(n=200\) 之后进入了一个我们定的小边界（用虚线表示），之后我们可以确定，它再也不会超出虚线所表示的边界（超出这个边界的概率是0）。跟上面的例子一样，虚线所表示的边界可以定得任意小，而一定会有一个n值，当这个数列超过了n值之后，超出这个边界的概率就是0了。

注意上面依概率收敛中有一句“不能保证，有没有哪一个数列会在未来再次超出虚线的范围然后再回来——虽然概率很小”，这个很重要，因为完全有可能有一个序列是这样的（我后面把这种序列叫做“刺头序列”吧）：

这个序列大趋势是 \(X_n=1/n\)，但是每过一段时间就有一个刺头跳出来。我们不能说 \(\lim_{n\to\infty}X_n=0\)，这是因为序列极限的定义为：若若对于任意 \(\varepsilon > 0\)，都存在一个 \(N\) 使得 \(|X_m-\mu| < \varepsilon,\forall m > N\)，则 \(\lim_{n\to\infty} X_n=\mu\)。但是对于上面这个例子呢？如果 \(\varepsilon < 0.2\)，我们就找不到这样一个 \(N\) 满足条件。

弱大数定律中允许存在这样的“刺头序列”，甚至全部是这种刺头序列也没关系，只要保证你们的“刺头”别挤在一块，偶尔出来跳一下，这样计算一个概率以后，有刺头出现的概率会随着 \(n\to\infty\) 而趋向于 0。

强大数定律中则不允许这样的刺头序列（应该说刺头序列出现的概率是 0），他要求每个序列的极限都一定是 \(\mu\)。

那么为什么把概率和极限交换一个位置就会出现强弱大数定理的这种差别呢？问题就出在极限 \(\lim\) 的定义了，当 \(\lim\) 在内部的时候，我们是盯着每一个序列看到了无穷远处，然后发现这个序列并不会有刺头跳出来，也就是说每个序列都有很好的性质。而当 \(\lim\) 在外部的时候，我们是先求了一个概率，然后再看到无穷远处，那么我们只知道求概率以后几乎没有刺头，谁知道中间有没有滥竽充数的呢？甚至可能所有序列都是滥竽充数的，只不过 \(n\) 的时候是序列 \(a\) 跳出来，\(n+1\) 的时候是序列 \(b\)，\(n+2\) 的时候是序列 \(c\) ……