凸优化笔记18:近似点算子 Proximal Mapping
前面讲了梯度下降法,分析了其收敛速度,对于存在不可导的函数介绍了次梯度的计算方法以及次梯度下降法,这一节要介绍的内容叫做近似点算子(Proximal mapping),也是为了处理非光滑问题。
1. 闭函数
在引入闭函数(closed function)的概念之前,我们先回顾一下闭集的概念:集合 \(\mathcal{C}\) 是闭的,如果它包含边界,也即 \[ x^{k} \in \mathcal{C}, \quad x^{k} \rightarrow \bar{x} \quad \Rightarrow \quad \bar{x} \in \mathcal{C} \] 并且有以下几个简单的原则可以保持集合闭的性质:
- 闭集的交集还是闭集;
- 有限个闭集的并集还是闭集;
- 如果 \(\mathcal{C}\) 是闭集,则线性映射的原象也是闭集,也即 \(\{x|Ax\in\mathcal{C}\}\) 是闭集。
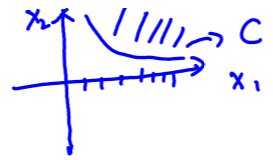
第 3 条原则反过来则不一定成立,也即如果 \(x\in\mathcal{C}\) 是闭集,那么 \(\{Ax|x\in\mathcal{C}\}\) 则不一定是闭集,比如我们可以取函数 \(f(x)=1/x\) 的 epigraph 为闭集 \(\mathcal{C}\),然而 \((x,y)\) 向 \(x\) 轴的投影则是一个开集,严格表示与图示如下 \[ \mathcal{C}=\left\{\left(x_{1}, x_{2}\right) \in \mathbb{R}_{+}^{2} | x_{1} x_{2} \geq 1\right\}, \quad A=[1,0], A \mathcal{C}=\mathbb{R}_{++} \]
| 第3条逆原则反例 | 第3条逆原则充分条件 |
|---|---|
 |
 |
当然,如果加一些其他的约束条件,则可以保证第 3 条反过来也成立:\(A\mathcal{C}\) 是闭的,如果
- \(\mathcal{C}\) 是闭的且为凸集;
- 并且 \(\mathcal{C}\) 不存在一个可以无穷延伸的方向(recession direction)属于 \(A\) 的零空间,也即 \(A y=0, \hat{x} \in \mathcal{C}, \hat{x}+\alpha y \in \mathcal{C}, \forall \alpha>0 \Rightarrow y=0\),图示即如上。
然后我们就可以定义闭函数(closed function)了,函数 \(f\) 为闭的,如果他的 epigraph 为闭集或者他的所有下水平集为闭集。有以下两种简单的特殊情况:
- 如果 \(f\) 连续且定义域 \(\text{dom}f\) 为闭的,则 \(f\) 为闭函数;
- 如果 \(f\) 连续且定义域 \(\text{dom}f\) 为开的,则 \(f\) 为闭函数当且仅当其在 \(\text{dom}f\) 边界处收敛至 \(\infty\)。
例子 1:\(f(x)=x\log x,\quad\text{dom}f=R_+,f(0)=0\)
例子 2:闭集的指示函数 \(\delta_C(x)=\begin{cases}0&x\in C\\ +\infty & o.w.\end{cases}\)
反例 3:\(f(x)=x\log x,\quad\text{dom}f=R_{++}\) 或者 \(f(x)=x\log x,\quad\text{dom}f=R_+,f(0)=1\) 不是闭函数
反例 4:开集的指示函数不是闭函数
闭函数有一些有用的性质,比如:
- \(f\) 为闭函数当且仅当他的所有下水平集都是闭集;
- 如果 \(f\) 为闭函数,且下水平集有界,那么存在最小值点(minimizer)。
Theorem (Weierstrass) :假设集合 \(D\subset \mathcal{E}\) (\(R^n\)空间中有限维向量子空间) 非空且闭,并且连续函数 \(f:D\to R\) 的所有下水平集都有界,则 \(f\) 存在全局最小值点(global minimizer)。
对于闭函数来说也有一些原则可以保持闭的性质:
- 如果 \(f,g\) 均为闭函数,则 \(f+g\) 为闭函数
- 如果 \(f\) 为闭函数,则 \(f(Ax+b)\) 为闭函数
- 如果任意 \(f_\alpha\) 都是闭函数,则 \(\sup_\alpha f_\alpha(x)\) 为闭函数
2. 共轭函数
共轭函数(conjugate function) 前面已经讲过了,这里再简单回顾一遍。函数 \(f\) 的共轭函数定义为 \[ f^\star(y)=\sup_{x\in\text{dom}f} (y^Tx-f(x)) \]
并且共轭函数有一些重要的性质:
- 共轭函数一定是闭函数,且为凸函数,不论 \(f\) 是否为凸函数或闭函数(因为 \(f^\star\) 的 epigraph 可以看成很多个半空间的交集);
- (Fenchel’s inequality) \(f(x)+f^{\star}(y) \geq x^{\top} y, \forall x, y\)
- (Legendre transform) 如果 \(f\) 为凸函数且为闭函数,则有 \(y \in \partial f(x) \Leftrightarrow x \in \partial f^{\star}(y) \Leftrightarrow x^{\top} y=f(x)+f^{\star}(y)\)
- 如果 \(f\) 为凸函数且为闭函数,则 \(f^{\star\star}=f\)
除此之外还有一些代数变换的原则,推导也都比较简单:
- \(f\left(x_{1}, x_{2}\right)=g\left(x_{1}\right)+h\left(x_{2}\right), \quad f^{\star}\left(y_{1}, y_{2}\right)=g^{\star}\left(y_{1}\right)+h^{\star}\left(y_{2}\right)\)
- \(f(x)=\alpha g(x), \quad f^{\star}(y) {=} \alpha g^{\star}(y / \alpha) \quad(\bigstar)\)
- \(f(x)=g(x)+a^{\top} x+b \quad f^{\star}(y)=g^{\star}(y-a)-b\)
- \(f(x)=\inf _{u+v=x}(g(u)+h(v)) \quad f^{\star}(y)=g^{\star}(y)+h^{\star}(y)\)
共轭函数的计算就不多举例子了,这里主要列出来后面用的比较多的而且比较重要的,其他的可以参考前面的笔记 6:
例子 1:\(C\) 为凸集,则指示函数 \(f(x)=\delta_C(x)\),其共轭函数为支撑函数 \[ f^\star(y) = \sup\{y^Tx|x\in C\} \] 如果求两次共轭函数也很容易得到:支撑函数的共轭函数为指示函数。
例子 2:范数 \(f(x)=\Vert x\Vert\) 的共轭函数也是指示函数 \[ f^\star(y) = \left\{\begin{array}{ll} 0 & \|y\|_{*} \leq 1 \\ \infty & \text { otherwise } \end{array}\right. \]
3. 近似点算子
首先给出来近似点算子(Proximal mapping)的定义:闭凸函数 \(f\) 的近似点算子定义为 \[ \operatorname{prox}_{f}(x)=\underset{u}{\operatorname{argmin}}\left(f(u)+\frac{1}{2}\|u-x\|_{2}^{2}\right) \] 根据这个定义,实际上我们是在求解函数 \(g(u)=f(u)+\frac{1}{2}\|u-x\|_{2}^{2}\) 的最小值,由于 \(g\) 是闭函数且下水平集有界,因此最小值一定存在;同时由于 \(g\) 为强凸函数,因此最小值点唯一。
那么怎么理解这个算子函数 \(\text{prox}_f(x)\) 呢?可以看到这实际上是一个 \(\text{prox}_f:R^n\to R^n\) 的映射。如果 \(u=\text{prox}_f(x)\),则应该有 \(x-u\in \partial f(u)\)。下面看一些简单的例子。
例子 1:二次函数 \(A\succeq 0\) \[ f(x)=\frac{1}{2} x^{T} A x+b^{T} x+c, \quad \operatorname{prox}_{t f}(x)=(I+t A)^{-1}(x-t b) \] 例子 2:欧几里得范数 \(f(x)=\Vert x\Vert_2\) \[ \operatorname{prox}_{t f}(x)=\left\{\begin{array}{ll} \left(1-t /\|x\|_{2}\right) x & \|x\|_{2} \geq t \\ 0 & \text { otherwise } \end{array}\right. \] 例子 3:Logarithmic barrier \[ f(x)=-\sum_{i=1}^{n} \log x_{i}, \quad \operatorname{prox}_{t f}(x)_{i}=\frac{x_{i}+\sqrt{x_{i}^{2}+4 t}}{2}, \quad i=1, \ldots, n \]
上面是比较简单的例子,近似点算子也有一些很容易验证的代数运算规律:
- \(f\left(\left[\begin{array}{l} x \\ y \end{array}\right]\right)=g(x)+h(y), \quad \operatorname{prox}_{f}\left(\left[\begin{array}{l} x \\ y \end{array}\right]\right)=\left[\begin{array}{l} \operatorname{prox}_{g}(x) \\ \operatorname{prox}_{h}(y) \end{array}\right]\)
- \(f(x)=g(a x+b), \quad \operatorname{prox}_{f}(x)=\frac{1}{a}\left(\operatorname{prox}_{a^{2} g}(a x+b)-b\right)\) (注意 \(a\ne0\) 是标量)
- \(f(x)=\lambda g(x / \lambda), \quad \operatorname{prox}_{f}(x)=\lambda \operatorname{prox}_{\lambda^{-1} g}(x / \lambda) \quad(\bigstar)\)
- \(f(x)=g(x)+a^{T} x, \quad \quad \operatorname{prox}_{f}(x)=\operatorname{prox}_{g}(x-a)\)
- \(f(x)=g(x)+\frac{\mu}{2}\|x-a\|_{2}^{2}, \quad \operatorname{prox}_{f}(x)=\operatorname{prox}_{\theta g}(\theta x+(1-\theta) a)\),其中 \(\mu>0,\theta=1/(1+\mu)\)
- \(f(x)=g(Ax+b)\),对于一般的 \(A\) 并不能得到比较好的性质,但如果 \(AA^T=(1/\alpha)I\),则有
\[ \begin{aligned}\operatorname{prox}_{f}(x) &=\left(I-\alpha A^{T} A\right) x+\alpha A^{T}\left(\operatorname{prox}_{\alpha^{-1} g}(A x+b)-b\right) \\&=x-\alpha A^{T}\left(A x+b-\operatorname{prox}_{\alpha^{-1} g}(A x+b)\right)\end{aligned} \]
前面几条都比较容易证明,最后一条证明可以等价于求解 \[ \begin{aligned}\text { minimize } \quad& g(y)+\frac{1}{2}\|u-x\|_{2}^{2}\\\text { subject to } \quad& A u+b=y\end{aligned} \] 可以先求解 \(x\) 向超平面 \(Au+b=y\) 投影来消去 \(u\),然后再计算 \(\text{prox}_f(y)\)。
除此之外,有一个非常重要的等式:
Moreau decomposition: \[ x=\operatorname{prox}_{f}(x)+\operatorname{prox}_{f^{*}}(x) \quad\text { for all } x \]
Remarks:为什么说这个式子重要呢?因为他把原函数和共轭函数的 proximal mapping 联系起来了,如果其中一个比较难计算,那么我们可以通过另一个来计算。这个式子可以怎么理解呢?可以看成是一种正交分解,举个栗子,如果我们取一个子空间 \(L\),他的正交空间为 \(L^\perp\),令函数 \(f\) 为子空间 \(L\) 的指示函数也即 \(f=\delta_L\),那么很容易验证共轭函数 \(f^\star=\delta_{L^\perp}\)。而根据定义也可以得到 \(\text{prox}_f(x)\) 恰好就是 \(x\) 在子空间 \(L\) 上的投影,记为 \(P_L(x)=\text{prox}_f(x)\),同样的 \(P_{L^\perp}(x)=\text{prox}_{f^\star}(x)\),因此上面的 Moreau decomposition 就可以写为 \(x=P_L(x)+P_{L^\perp}(x)\),这正好就是一个正交分解。可以根据下图理解

如果对原始的 Moreau decomposition 做简单的代数变换,就可以得到 \(\lambda>0\) \[ x=\operatorname{prox}_{\lambda f}(x)+\lambda \operatorname{prox}_{\lambda^{-1} f^{*}}(x / \lambda) \quad \text { for all } x \] 证明过程用到了共轭函数的性质 \((\lambda f)^{\star}(y)=\lambda f^{\star}(y / \lambda)\)。
后面两个小节则主要是近似点算子的应用,一个是计算投影,另一个是与支撑函数、距离相关的内容。
4. 投影
为什么突然讲到投影呢?因为对指示函数应用近似点算子,实质上就是在计算投影。举个栗子就明白了:对于集合 \(C\) 与集合外一点 \(x\),\(x\) 向集合 \(C\) 的投影可以表示为 \[ \begin{aligned}\text { minimize } \quad& \frac{1}{2}\|y-x\|_{2}^{2}\\\text { subject to } \quad& y\in C\end{aligned} \] 若投影点为 \(y^\star\),则这可以等价表示为 \[ \begin{aligned}y^\star &= \arg\min_y \frac{1}{2}\|y-x\|_{2}^{2}+\delta_C(y) \\&= \text{prox}_{\delta}(x)\end{aligned} \] 因此 \(\text{prox}_{\delta}(x)\) 就是 \(x\) 向集合 \(C\) 的投影点(对于 \(x\in C\) 同样成立)。那么只要我们取不同的 \(C\),就能得到各种类型集合的投影表达式,下面举一些例子。
超平面:\(C=\{x|a^Tx=b\}\) with \(a\ne0\) \[ P_{C}(x)=x+\frac{b-a^{T} x}{\|a\|_{2}^{2}} a \] 仿射集:\(C=\{x | A x=b\}\left(\text { with } A \in \mathbf{R}^{p \times n} \text { and } \operatorname{rank}(A)=p\right)\) \[ P_{C}(x)=x+A^{T}\left(A A^{T}\right)^{-1}(b-A x) \] 半空间:\(C=\{x|a^Tx\le b\}\) with \(a\ne0\) \[ P_{C}(x)=\begin{cases}x+\frac{b-a^{T} x}{\|a\|_{2}^{2}} a & \text {if } a^{T} x>b \\ x & \text {if } a^{T} x \leq b\end{cases} \] 矩形:\(C=[l, u]=\left\{x \in \mathbf{R}^{n} | l \leq x \leq u\right\}\) \[ P_{C}(x)_{k}=\left\{\begin{array}{ll}l_{k} & x_{k} \leq l_{k} \\x_{k} & l_{k} \leq x_{k} \leq u_{k} \\u_{k} & x_{k} \geq u_{k}\end{array}\right. \] 非负象限:\(C=R_+^n\) \[ P_{C}(x)=x_{+}=\left(\max \left\{0, x_{1}\right\}, \max \left\{0, x_{2}\right\}, \ldots, \max \left\{0, x_{n}\right\}\right) \] 概率单形:\(C=\left\{x | \mathbf{1}^{T} x=1, x \geq 0\right\}\) \[ P_{C}(x)=(x-\lambda \mathbf{1})_{+} \] 其中 \(\lambda\) 由以下方程解出 \[ \mathbf{1}^{T}(x-\lambda \mathbf{1})_{+}=\sum_{i=1}^{n} \max \left\{0, x_{k}-\lambda\right\}=1 \] 这个的证明有一点难度,关键是首先要把约束条件 \(x\ge0\) 转换为指示函数表示 \[ \begin{aligned}\text { minimize } \quad& \frac{1}{2}\|y-x\|_{2}^{2} + \delta_{R_+^n}(y) \\\text { subject to } \quad& \mathbf{1}^{T} y=1\end{aligned} \] 然后将拉格朗日函数分解成求和的形式 \[ \begin{array}{l}\frac{1}{2}\|y-x\|_{2}^{2}+\delta_{\mathbf{R}_{+}^{n}}(y)+\lambda\left(\mathbf{1}^{T} y-1\right) \\\quad=\quad \sum_{k=1}^{n}\left(\frac{1}{2}\left(y_{k}-x_{k}\right)^{2}+\delta_{\mathbf{R}_{+}}\left(y_{k}\right)+\lambda y_{k}\right)-\lambda\end{array} \] 对上面这个求和项进行分情况讨论就能得到解析表达式了,不过真的很繁琐。
超平面与矩形交集:\(C=\{x|a^Tx=b,l\preceq x\preceq u\}\) \[ P_{C}(x)=P_{[l,u]}(x-\lambda a) \] 其中 \(\lambda\) 由以下方程解出 \[ a^{T} P_{[l, u]}(x-\lambda a)=b \] 证明跟上面的概率单形是类似的,也需要拆写成多项求和的形式分别求解。
欧几里得球:\(C=\{x| \Vert x\Vert_2\le1\}\) \[ P_{C}(x)=\begin{cases}\frac{x}{\|x\|_{2}} & \text {if } \Vert x\Vert_2>1 \\ x & \text {if } \Vert x\Vert_2\le1\end{cases} \] 1 范数球:\(C=\{x| \Vert x\Vert_1\le1\}\)
若 \(\Vert x\Vert_1\le1\) 则 \(P_C(x)=x\);否则 \[ P_{C}(x)_{k}=\operatorname{sign}\left(x_{k}\right) \max \left\{\left|x_{k}\right|-\lambda, 0\right\}=\left\{\begin{array}{ll}x_{k}-\lambda & x_{k}>\lambda \\0 & -\lambda \leq x_{k} \leq \lambda \\x_{k}+\lambda & x_{k}<-\lambda\end{array}\right. \] 其中 \(\lambda\) 由以下等式获得 \[ \sum_{k=1}^n \max \{\vert x\vert_k-\lambda, 0\}=1 \] 证明业与前面的类似,需要写成求和项的形式,然后对每一项求解。
二阶锥:\(C=\{(x,t)\in R^{n\times 1}| \Vert x\Vert_2 \le t \}\) \[ P_{C}(x,t)=\begin{cases}(x,t) & \text {if } \Vert x\Vert_2\le t \\ (0,0) & \text {if } \Vert x\Vert_2\le -t \\\frac{t+\|x\|_{2}}{2\|x\|_{2}}\left[\begin{array}{c} x \\ \|x\|_{2} \end{array}\right] & \text {if } \Vert x\Vert_2> \vert t\vert \end{cases} \] 正定锥:\(C=S^n_+\) \[ P_{C}(X)=\sum_{i=1}^{n} \max \left\{0, \lambda_{i}\right\} q_{i} q_{i}^{T} \] 其中 \(X=\sum_i \lambda_i q_iq_i^T\)
5. 支撑函数、范数与距离
这一小节标题看起来很复杂,牵涉到了支撑函数、范数、到集合的距离,但实际上都还是在计算投影,为什么这么说呢?回忆一下,支撑函数的共轭函数是不是 \(\delta\) 函数?范数的共轭函数是不是 \(\delta\) 函数?到集合的距离是不是就等于到投影点的距离?所以这一小节是上一小节“投影”的自然延伸,其中为了把原函数与共轭函数联系在一起,用到了 Moreau decomposition。我们一个一个来看。 \[ x=\operatorname{prox}_{f}(x)+\operatorname{prox}_{f^{*}}(x) \quad\text { for all } x \] 支撑函数:\(f(x)=\sup_{y\in C}x^Ty,f^\star(y)=\delta_C(y)\),因此近似点算子为 \[ \begin{aligned}\operatorname{prox}_{t f}(x) &=x-t \operatorname{prox}_{t^{-1} f^{*}}(x / t) \\&=x-t P_{C}(x / t)\end{aligned} \] 范数:\(f(x)=\Vert x\Vert,f^\star(y)=\delta_B(y)\),其中 \(B=\{y| \Vert y\Vert_\star \le 1\}\),近似点算子为 \[ \begin{aligned}\operatorname{prox}_{t f}(x) &=x-t \operatorname{prox}_{t^{-1} f^{*}}(x / t) \\&=x-t P_{B}(x / t) \\&=x- P_{tB}(x)\end{aligned} \] 其中 \(tB=\{y| \Vert y\Vert_\star \le t\}\)
与一点的距离:\(f(x)=\Vert x-a\Vert\),可以取 \(g(x)=\Vert x\Vert\) \[ \begin{aligned}\operatorname{prox}_{t f}(x) &=a + \operatorname{prox}_{tg}(x-a) \\&=a+x-a-tP_B(\frac{x-a}{t}) \\&=x- P_{tB}(x-a)\end{aligned} \] 到集合的距离:到闭凸集 \(C\) 的距离定义为 \(d(x)=\inf_{y\in C}\Vert x-y\Vert_2\) \[ \operatorname{prox}_{t d}(x)=\left\{\begin{array}{ll}x+\frac{t}{d(x)}\left(P_{C}(x)-x\right) & d(x) \geq t \\P_{C}(x) & \text { otherwise }\end{array}\right. \] 如果是距离取平方 \(f(x)=d(x)^2/2\),则有 \[ \operatorname{prox}_{t f}(x)=\frac{1}{1+t} x+\frac{t}{1+t} P_{C}(x) \] 这个证明贴在下面

