凸优化笔记 2:超平面分离定理
简单理解就是:没有交集的两个凸集,可以被一个超平面完全分隔开。
1. 超平面分离定理
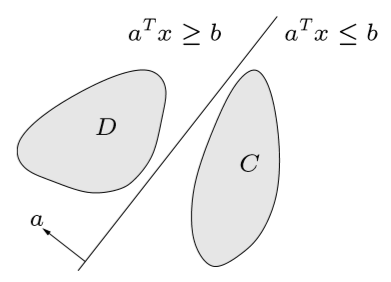
超平面分离定理(Separating hyperplane theorem):若 \(C,D\) 为非空凸集,且 \(C\cap D=\varnothing\),则存在 \(a\ne 0,b\),使得 \[ a^Tx\le b\quad\text{for}\quad x\in C,\quad a^Tx\ge b \quad\text{for}\quad x\in D \] 也可以等价表示为 \(\inf_{x\in D}a^Tx \ge \sup_{x\in C}a^Tx\)
Lemma 1:\(C\) closed,convex,\(y\notin C\),那么存在唯一的 \(x\in C\),使得 \(\Vert y-x\Vert=\inf\{\Vert y-z\Vert|z\in C\}=d(y,C)\)
Proof:omit...
Lemma 2:\(C\) closed,convex,\(y\notin C\),那么存在 \(a\ne 0,b\),使得 \[ a^Ty<b,\quad a^Tx\ge b\quad\forall x\in C \] Proof:omit...
Remark:上述定理表明存在超平面可以严格分开 \(y\) 与 \(C\)。
Lemma 3:\(C\) convex,\(y\notin C\),那么存在 \(a\ne 0,b\),使得 \[ a^Ty\le b,\quad a^Tx\ge b\quad\forall x\in C \] Proof:omit...
超平面分离定理逆定理:若 \(C\) 为开集,且存在超平面分离 \(C,D\),则 \(C\cap D=\varnothing\)
2. 支撑超平面定理
支撑超平面:对于集合 \(C\) 的边界点 \(x_0\),支撑超平面为 \(\{x|a^Tx=a^Tx_0\}\),其满足 \(a\ne0\) 且 \(a^Tx\le a^Tx_0,\ \forall x\in C\)
支撑超平面定理:如果 \(C\) 为凸集,那么 \(C\) 的每个边界点都存在一个支撑超平面