凸优化笔记 3:广义不等式
将普通的不等式 \(1\le2\) 推广到更加复杂的情况,例如两个向量 \(x\le y\) 该如何定义?这就是广义不等式(generalized inequality)
1. 正常锥
正常锥(proper cone) \(K\subseteq R^n\) 需要满足
- \(K\) is closed (contains its boundary)
- \(K\) is solid (has nonempty interior)
- \(K\) is pointed (contains no line)
2. 广义不等式
基于正常锥 \(K\) 定义的不等式(generalized inequality)表示为 \[ x \preceq_{K} y \quad \Longleftrightarrow \quad y-x \in K \\ x \prec_{K} y \quad \Longleftrightarrow \quad y-x \in \operatorname{int} K \]
3. 最小元与极小元
3.1 最小元(minimum)
\(x\in S\) 为集合 \(S\) 关于 \(\preceq_{K}\) 的最小元(minimum),如果有 \[ y\in S \Longrightarrow x\preceq_{K}y \] 也等价于 \(S\subseteq x+K\)
注意:1. 最小元可能不存在;2. 若存在则唯一
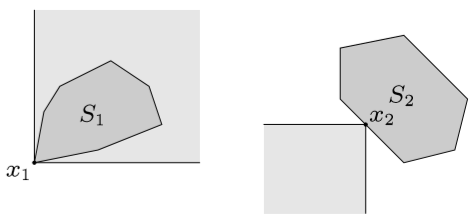
3.2 极小元(minimal)
\(x\in S\) 为集合 \(S\) 关于 \(\preceq_{K}\) 的极小元(minimum),如果有 \[ y\in S\quad y\preceq_{K}x \Longrightarrow y=x \] 注意:极小元不唯一
4. 对偶锥
锥 \(K\) 的对偶锥(dual cone) 定义为 \[ K^{*}=\left\{y | y^{T} x \geq 0 \text { for all } x \in K\right\} \] 有一些性质
- \(K^*\) is convex, closed
- \(K^{**}=K\) if \(K\) is closed convex
- \(K\) is proper cone \(\Longrightarrow K^{*}\) is proper
一些例子
- \(K=\mathbf{R}_{+}^{n}: K^{*}=\mathbf{R}_{+}^{n}\)
- \(K=\mathbf{S}_{+}^{n}: K^{*}=\mathbf{S}_{+}^{n}\)
- \(K=\left\{(x, t) |\|x\|_{2} \leq t\right\}: K^{*}=\left\{(x, t) |\|x\|_{2} \leq t\right\}\)
- \(K=\left\{(x, t) |\|x\|_{1} \leq t\right\}: K^{*}=\left\{(x, t) |\|x\|_{\infty} \leq t\right\}\)
5. 最小元与极小元(应用对偶锥定义)
5.1 最小元
\(x\) 是集合 \(S\) 关于 \(\preceq_{K}\) 的最小元 \(\iff\) 对任意的 \(\lambda \succ_{K*} 0\),\(x\) 为 \(\lambda^Tz\) 在集合 \(S\) 上的唯一最小解
Remarks:实际上这点可以理解为对任意 \(\lambda\in K^*\),其定义了一个支撑超平面,\(x\) 就是支撑点
5.2 极小元
- 充分条件:若对于某些 \(\lambda \succ_{K*} 0\),\(x\) minimizes \(\lambda^Tz\) over \(S\),\(\Longrightarrow\) \(x\) 为极小元
- 必要条件:\(x\) 为凸集 \(S\) 的极小元,\(\Longrightarrow\) 存在非 0 的 \(\lambda \succ_{K*} 0\) 使得 \(x\) minimizes \(\lambda^Tz\) over \(S\)