模糊数学笔记 1:模糊集 Fuzzy set
传统集合中元素要么属于集合,要么不属于集合。但假如我们给出一个“所有年轻人组成的集合”,那么这个时候年龄多大才算年轻人呢?30岁算年轻人嘛?有的人觉得算,有的人觉得不算,这是一个比较模糊的界定,所以就引入了模糊集的概念。
1. 传统集合的定义
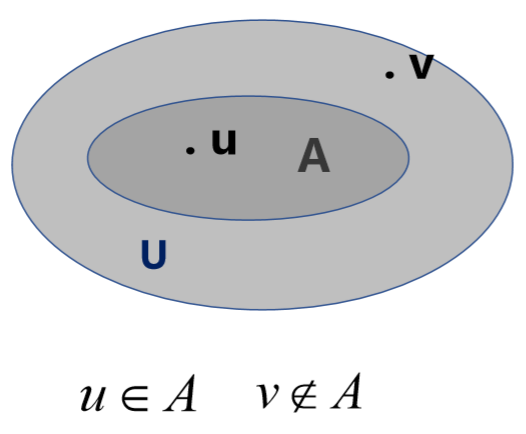
论域 U,集合
A,这可以用一个映射来表示 \[
\begin{aligned}
\chi_{A}: \boldsymbol{U} \rightarrow &\{\mathbf{0}, \mathbf{1}\} \\
\boldsymbol{u} \mapsto & \chi_{A}(\boldsymbol{u})
\end{aligned}
\] 也可以用一个分段函数来表示 \[
\chi_{A}(u)=\left\{\begin{array}{ll}
{1,} & {u \in A} \\
{0,} & {u \notin A}
\end{array}\right.
\] 
2. 模糊集合的定义
模糊集的含义表示其中的元素 \(x\) “有一定的可能性”属于集合 \(A\),或者说“一定程度上”属于集合 \(A\),那么这个属于的程度就被称为隶属度 \(\mu_A(x)\in [0,1]\)。与传统集合相比,传统集合中元素的隶属程度非 0 即 1,也即要么属于,要么不属于,是确定的,模糊集里则引入了一定的不确定性。也用一个映射表示为 \[ \begin{aligned} \mu_{A}: &\boldsymbol{U} \rightarrow[0,1] \\ &\boldsymbol{x} \mapsto \mu_{A}(x) \in[0,1] \end{aligned} \] 其中映射 \(\mu_A\) 称为 \(A\) 的隶属函数,\(\mu_A(x)\) 为 \(x\) 对 \(A\) 的隶属度。注意 \(\mu_A(x)=0.5\) 时表示最具有模糊性。
3. 模糊集的表示方法
3.1 Zadeh 表示法
\[ A=\frac{A\left(x_{1}\right)}{x_{1}}+\frac{A\left(x_{2}\right)}{x_{2}}+\cdots+\frac{A\left(x_{n}\right)}{x_{n}} \]
这里 \(\frac{A\left(x_{i}\right)}{x_{i}}\) 表示 \(x_i\) 对模糊集 \(A\) 的隶属度为 \(A(x_i)\)。若论域 \(U\) 为无限集,则模糊集表示为 \[ A=\int_{x\in U} \frac{A(x)}{x} \]
3.2 序偶表示法
\[ A=\left\{\left(x_{1}, A\left(x_{1}\right)\right),\left(x_{2}, A\left(x_{2}\right)\right), \cdots,\left(x_{n}, A\left(x_{n}\right)\right)\right\} \]
3.3 向量表示法
\[ A=(A(x_1),...,A(x_n)) \]
4. 模糊集的运算
4.1 集合基本运算
- 相等:\(A=B \iff A(x)=B(x), \forall x\in U\)
- 包含:\(A\subset B \iff A(x)\le B(x), \forall x\in U\)
- 交集:\((A\cap B)(x) = A(x)\wedge B(x),\forall x\in U\)
- 并集:\((A\cup B)(x) = A(x)\vee B(x),\forall x\in U\)
- 补集:\(A^c(x)=1-A(x),\forall x\in U\)
其中记号 \(a\wedge b=\min\{a,b\},a\vee b=\max\{a,b\}\)
4.2 计算性质
很多计算性质都和普通集合差不多
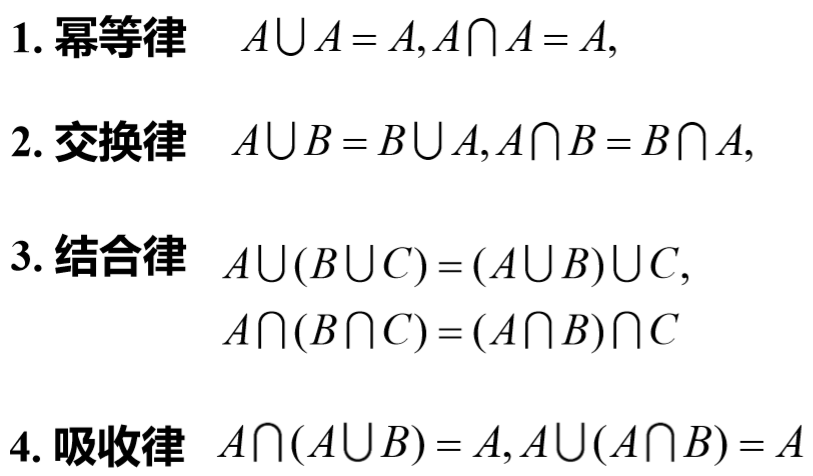
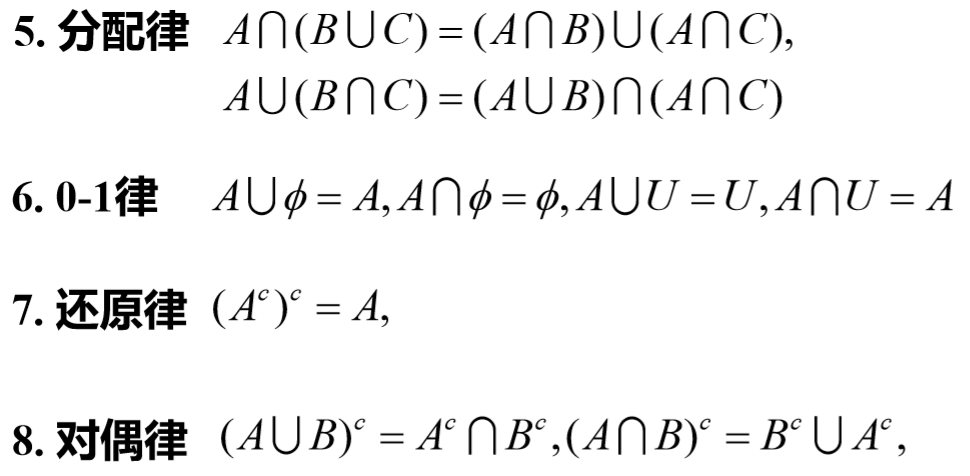
需要注意的是无穷个集合的交集与并集的定义 \[ \bigcup_{t \in T} A_{t}(a)=\sup_{t \in T} A_{t}(a) \\ \bigcap_{t \in T} A_{t}(a)=\inf_{t \in T} A_{t}(a) \]
5. 隶属度的确定
5.1 实验统计法
5.2 (半)解析法
根据问题性质套用现有模糊分布,然后根据测量数据确定分布中的参数。
模糊分布大致分为:偏大型、偏小型、中间型
5.3 专家打分法
根据专家的反馈意见进行统计
6. 截集与分解定理
6.1 截集的定义
定义:若 \(A\) 为 \(U\) 上的任一模糊集,对 \(\forall \lambda\in [0,1]\),记 \[ A_\lambda = \{x|A(x)\ge\lambda,x\in U\} \] 称为 \(A\) 的\(\lambda\)-截集,其中 \(\lambda\) 称为阈值或置信水平。类似的,强截集(开截集)定义为 \[ A_\lambda = \{x|A(x)>\lambda,x\in U\} \] 注意:截集为普通集合,不是模糊集!
6.2 截集运算性质
大部分性质都很简单
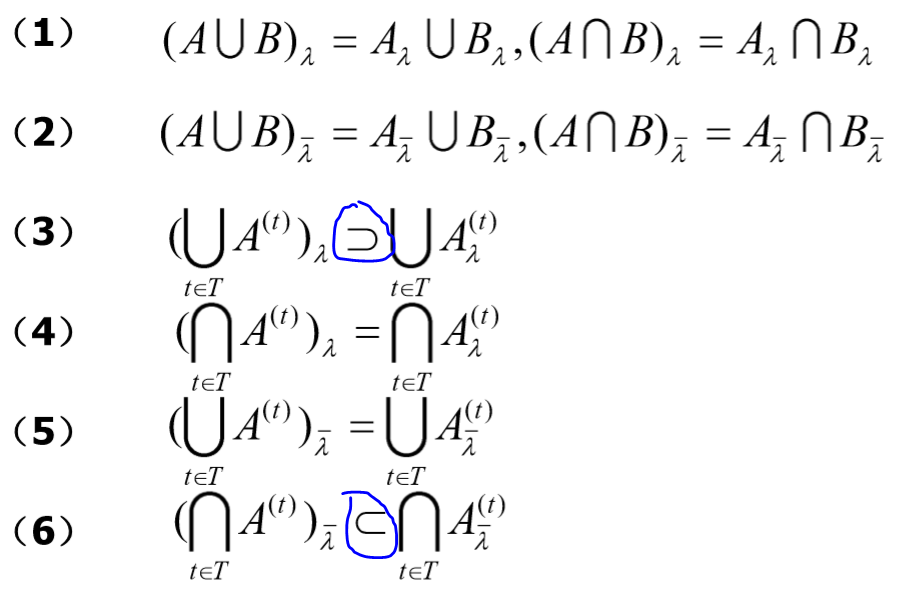
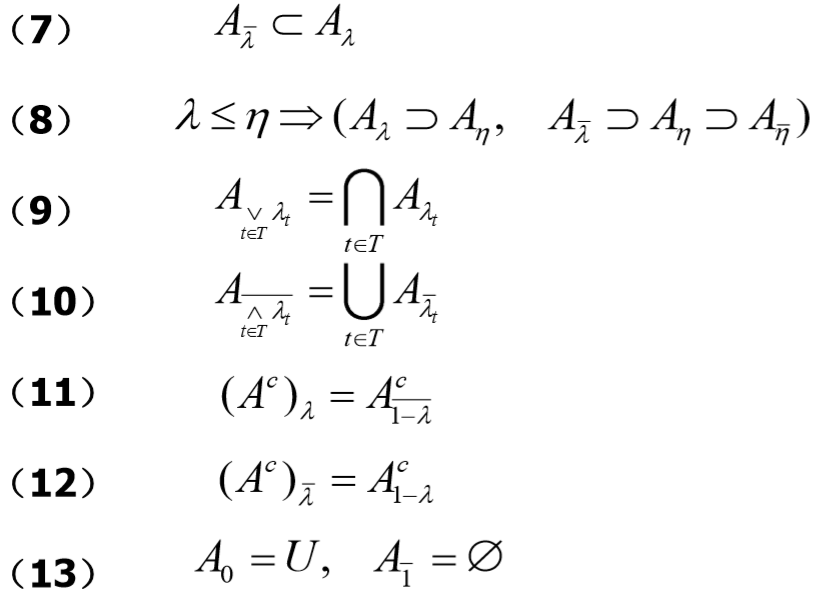
但注意其中第 3 和第 6 条注意并不是相等!!
6.3 一些定义
- 核:\(ker(A)=A_1\)
- 支集:\(supp(A)=A_{\bar{0}}\)
- 边界:\(A_{\bar{0}}\backslash A_1\)
- 数乘:\(\lambda A(u) =
\lambda \wedge A(u),u\in U\)
- \(A\subset B \Rightarrow \lambda A \subset \lambda B\)
- \(\lambda_1\le\lambda_2\Rightarrow \lambda_1 A \subset \lambda_2 A\)
6.4 分解定理
分解定理 1:\(A\in \mathcal{F}(U)\),则 \(A=\bigcup_{\lambda\in[0,1]}\lambda A_\lambda\)
分解定理 2:\(A\in \mathcal{F}(U)\),则