PID 控制器
在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点.
1. 基本原理
PID控制器(比例-积分-微分控制器),由比例单元(P)、积分单元(I)和微分单元(D)组成。可以透过调整这三个单元的增益 \(K_p\),\(K_i\) 和 \(K_d\) 来调定其特性。PID控制器主要适用于基本上线性,且动态特性不随时间变化的系统。
PID控制器的比例单元(P)、积分单元(I)和微分单元(D)分别对应目前误差、过去累计误差及未来误差。若是不知道受控系统的特性,一般认为PID控制器是最适用的控制器。
2. 控制算法
若定义 \(u(t)\) 为控制输出,PID算法可以用下式表示 \[ \mathrm{u}(t)=\mathrm{MV}(t)=K_{p} e(t)+K_{i} \int_{0}^{t} e(\tau) d \tau+K_{d} \frac{d}{d t} e(t) \] 其中 \(e(t)\) 表示误差。
2.1 比例控件
比例控制考虑当前误差,误差值和一个正值的常数 \(K_p\)(表示比例)相乘。\(K_p\) 只是在控制器的输出和系统的误差成比例的时候成立。 \[ P_{\text{out}} = K_p e(t) \] 若比例增益大,在相同误差量下,会有较大的输出,但若比例增益太大,会使系统不稳定。相反的,若比例增益小,若在相同误差量下,其输出较小,因此控制器会较不敏感的。若比例增益太小,当有干扰出现时,其控制信号可能不够大,无法修正干扰的影响。
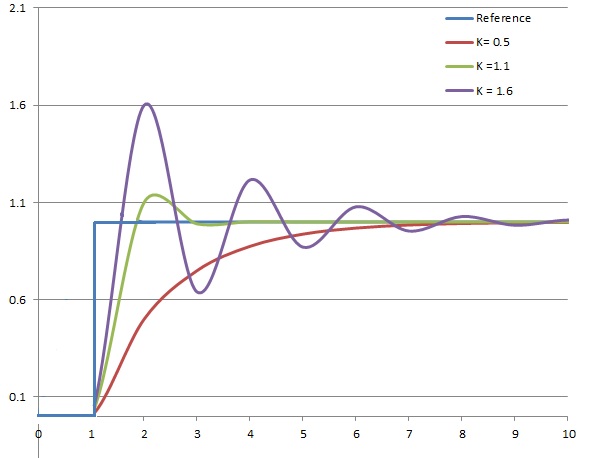
上图即为改变 \(K_p\) 对应的控制器。
2.2 积分控件
积分控制考虑过去误差,将误差值过去一段时间和(误差和)乘以一个正值的常数 \(K_i\)。 \[ I_{\mathrm{out}}=K_{i} \int_{0}^{t} e(\tau) d \tau \] 积分控制会加速系统趋近设定值的过程,并且消除纯比例控制器会出现的稳态误差。积分增益越大,趋近设定值的速度越快,不过因为积分控制会累计过去所有的误差,可能会使回授值出现过冲的情形。
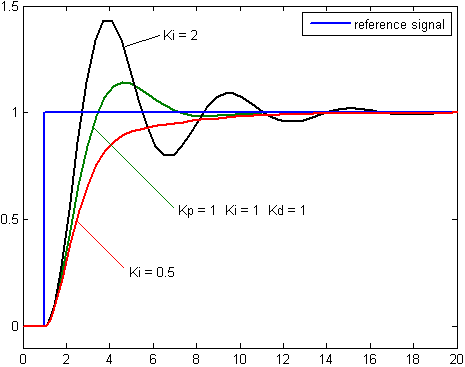
上图即为改变 \(K_i\) 对应的控制器。
2.3 微分控件
微分控制考虑将来误差,计算误差的一阶导,并和一个正值的常数 \(K_d\) 相乘。这个导数的控制会对系统的改变作出反应。导数的结果越大,那么控制系统就对输出结果作出更快速的反应。这个 \(K_d\) 参数也是PID被称为可预测的控制器的原因。\(K_d\) 参数对减少控制器短期的改变很有帮助。一些实际中的速度缓慢的系统可以不需要 \(K_d\) 参数。 \[ D_{\mathrm{out}}=K_{d} \frac{d}{d t} e(t) \] 微分控制可以提升整定时间及系统稳定性。不过因为纯微分器不是因果系统,因此在PID系统实现时,一般会为微分控制加上一个低通滤波器以限制高频增益及噪声。实际上较少用到微分控制,估计PID控制器中只有约20%有用到微分控制。
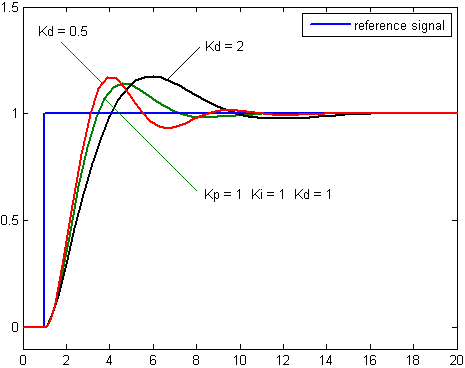
上图即为改变 \(K_d\) 对应的控制器。
3. 位置式和增量式PID算法
PID 一般有两种:位置式 PID 和增量式 PID。在小车里一般用增量式,因为位置式 PID 的输出与过去的所有状态有关,计算时要对历史上每一次的控制误差进行累加,这个计算量非常大,而且没有必要。增量式则子需要计算每次控制量的变化量。
将 PID 公式离散化,可以推导出位置式 PID 公式 \[ \begin{aligned} u(k)&=K_p\left[e_{k}+\frac{1}{T_i} \sum_{j=0}^{k} e_{j}+T_d \frac{e_{k}-e_{k-1}}{T}\right] \\ &=K_p \cdot e_{k}+\frac{K_p}{T_i} \sum_{j=0}^{k} e_{j}+K_p \cdot T_d \frac{e_{k}-e_{k-1}}{T} \\ &=A e_{k}+B\left(\sum_{j=0}^{k-1} e_{j}+e_{k}\right)+C\left(e_{k}-e_{k-1}\right) \end{aligned} \] 其中把 \(K_i,K_d\) 表示为 \(K_p/T_i,K_p\cdot T_d\)。
在此基础上可以推导出增量式 PID 公式 \[ \begin{aligned} \Delta u_{k}&=u_{k}-u_{k-1}=K_p\left[e_{k}-e_{k-1}+\frac{T}{T_i} e_{k}+T_d \frac{e_{k}-2 e_{k-1}+e_{k-2}}{T}\right] \\ &=K_p\left(1+\frac{T}{T_i}+\frac{T_d}{T}\right) e_{k}-K_p\left(1+\frac{2 T_d}{T}\right) e_{k-1}+K_p \frac{T_d}{T} e_{k-2} \\ &=A e_{k}+B e_{k-1}+C e_{k-2} \end{aligned} \] 其中误差 \(e_k = y_0(kT) - y(kT)\),\(y_0\) 表示目标值,\(y(kT)\) 表示第 \(k\) 个时刻的值。