LaSalle's invariance principle 拉萨尔不变性原理

拉萨尔不变原理是李亚普诺夫第二方法的推广。这种观察给出了李亚普诺夫理论的统一认识，且极大地推广了李亚普诺夫第二方法，现在人们称这一推广为拉萨尔不变原理。

1. 系统模型

考虑一个控制系统 \[ \dot{x}(t)=f(x(t)) \] 其中 \(f(0)=0\)。

2. 基本定义

正极限点(positive limit point)：p 被称为 \(x(t)\) 的正极限点，如果存在一个时间序列 \(\{t_n\}\)，有 \(n\to\infty\) 时 \(t_n\to\infty\)，且使得 \(x(t_n)\to\infty\) 随着 \(n\to\infty\)。

正极限集(positive limit set)：\(x(t)\) 的所有正极限点的集合即为正极限集。

Remarks：这里举个例子，序列 \(x(n)=1,-1,1,-1,...\)，那么取奇数项时极限为 1，偶数项时极限为 -1.但是对于完整的序列 \(x(n)\) 则极限不存在，而 \(x(n)\) 的正极限集则为 \(\{1,-1\}\)。

为什么这里会引入集合呢？因为控制系统中最终的稳定状态可能不是一个孤立的点，而是在很多个状态之间循环转换，比如一个单位圆。

不变集(invariant set)：集合 \(M\) 是关于系统 (1) 的不变集，如果有 \(x(0)\in M \Rightarrow x(t)\in M, \forall t\in \mathbb{R}\)。如果有 \(x(0)\in M \Rightarrow x(t)\in M, \forall t\ge0\) 则称为正不变集(positive invariant set)。

3. 拉萨尔不变性原理

LaSalle' Theorem：令 \(\Omega\in D\) 是一个紧致集，且是关于系统 \(\dot{x}(t)=f(x(t))\) 的不变集。令 \(V:D\to\mathbb{R}\) 是一个连续函数，且满足 \(\dot{V}(x)\le0\ \ in\ \ \Omega\)。令 \(M\) 为 \(\Omega\) 中所有满足 \(\dot{V}(x)=0\) 的点的集合，令 \(E\) 为 \(M\) 中的最大不变集，那么从 \(\Omega\) 中出发的所有解都将趋于 \(E\) 随着 \(t\to\infty\)。

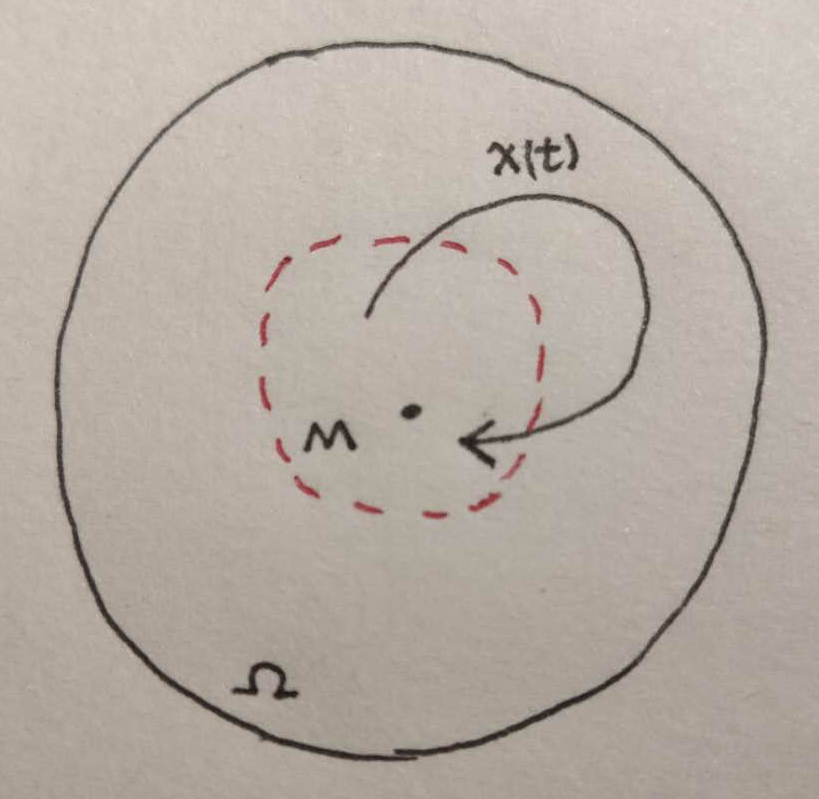
Remarks：这里的 \(M\) 和 \(E\) 有什么不同吗？二者不等价吗？不一定等价！因为 \(\Omega\) 本身是一个不变集，而 \(M\) 又是他的一个子集，如下图所示，那么任意一个起始于 \(M\) 的轨迹都有可能跑出 \(M\) 而进入 \(\Omega\backslash M\)，因此 \(M\) 并不是一个不变集。