统计推断(七) Typical Sequence

典型集

1. 一些定理

Markov inequality: \(r.v. \ \ \mathsf{x}\ge0\) \[ \mathbb{P}(x\ge\mu)\le \frac{\mathbb{E}[x]}{\mu} \] Proof: omit...

Weak law of large numbers(WLLN): \(\vec{y}=[y_1,y_2,...,y_N]^T, \ \ \ \ y_i \sim p \ \ \ i.i.d\) \[ \lim_{N\to\infty}\mathbb{P}(|L_p(\vec{y})+H(p)|>\varepsilon)=0, \ \ \forall \varepsilon>0 \] Proof: omit...

2. Typical set

• Definition: \(\mathcal{T}_\varepsilon(p;N)=\{\vec{y}\in\mathcal{Y}^N:|L_p(\vec{y})+H(p)|<\varepsilon\}\)

• Properties

  • WLLN \(\Longrightarrow P\left(\vec{y}\in\mathcal{T}_\varepsilon(p;N)\right)\simeq1\), \(N\) large
  • \(L_p(\vec{y})\simeq H(p) \Longrightarrow p_y(\vec{y})\simeq 2^{-NH(p)}\)
  • \(\Longrightarrow |\mathcal{T}_\varepsilon(p;N)|\simeq 2^{NH(p)}\)
  • 当 p 不是均匀分布的时候，\(\frac{|\mathcal{T}_\varepsilon(p;N)|}{|\mathcal{Y}^N|}\to0\)，也就是说典型集中元素(序列)个数在所有可能的元素(序列)中所占比例趋于 0，但是典型集中元素概率的和却趋近于 1

• Theorem

Asymptotic Equipartition Property(AEP)

• \[ \lim_{N\to\infty}P(\mathcal{T}_\varepsilon(p;N))=1 \\ \] \[ 2^{-N(H(p)+\epsilon)} \leq p_{\mathrm{y}}(\boldsymbol{y}) \leq 2^{-N(H(p)-\epsilon)}, \forall \boldsymbol{y} \in \mathcal{T}_{\epsilon}(p ; N) \]
• for a sufficient large \(N\) \[ (1-\epsilon) 2^{N(H(p)-\epsilon)} \leq\left|\mathcal{T}_{\epsilon}(p ; N)\right| \leq 2^{N(H(p)+\epsilon)} \] Proof: \[ \begin{aligned}\left|\mathcal{T}_{\epsilon}(p ; N)\right| &=\sum_{\boldsymbol{y} \in \mathcal{T}_{\epsilon}(p ; N)} 1 \\ &=2^{N(H(p)+\epsilon)} \sum_{\boldsymbol{y} \in \mathcal{T}_{\epsilon}(p ; N)} 2^{-N(H(p)+\epsilon)} \\ & \leq 2^{N(H(p)+\epsilon)} \sum_{\boldsymbol{y} \in \mathcal{T}_{\epsilon}(p ; N)} p_{\mathbf{y}}(\boldsymbol{y}) \\ &=2^{N(H(p)+\epsilon)} P\left\{\mathcal{T}_{\epsilon}(p ; N)\right\} \\ & \leq 2^{N(H(p)+\epsilon)} \end{aligned} \]

typical_set

3. Divergence \(\varepsilon\)-typical set

• WLLN: \(\vec{y}=[y_1,y_2,...,y_N]^T, \ \ \ \ y_i \sim p \ \ \ i.i.d\) $$ L_{p | q}()= = _{n=1}^{N} \

  {N } (|L{p | q}()-D(p | q)|>)=0 $$ Remarks: 前面只考虑的均值，这里还考虑了另一个分布

• Definition: \(\vec{\boldsymbol{y}}=[y_1,y_2,...,y_N]^T, \ \ \ \ y_i \sim p \ \ \ i.i.d\) \[ \mathcal{T}_{\epsilon}(p | q ; N)=\left\{\boldsymbol{y} \in \mathcal{Y}^{N}:\left|L_{p | q}(\boldsymbol{y})-D(p \| q)\right| \leq \epsilon\right\} \]

• Properties

  • WLLN \(\Longrightarrow q_{\mathbf{y}}(\boldsymbol{y}) \approx p_{\mathbf{y}}(\boldsymbol{y}) 2^{-N D(p \| q)}\)
  • \(Q\left\{\mathcal{T}_{\epsilon}(p | q ; N)\right\} \approx 2^{-N D(p \| q)} \to0\)
  • Remarks: p 的典型集可能是 q 的非典型集，在 \(N\) 很大的时候，不同分布的 typical set 是正交的

• Theorem \[ (1-\epsilon) 2^{-N(D(p \| q)+\epsilon)} \leq Q\left\{\mathcal{T}_{\epsilon}(p \| q ; N)\right\} \leq 2^{-N(D(p \| q)-\epsilon)} \]

4. Large deviation of sample averages

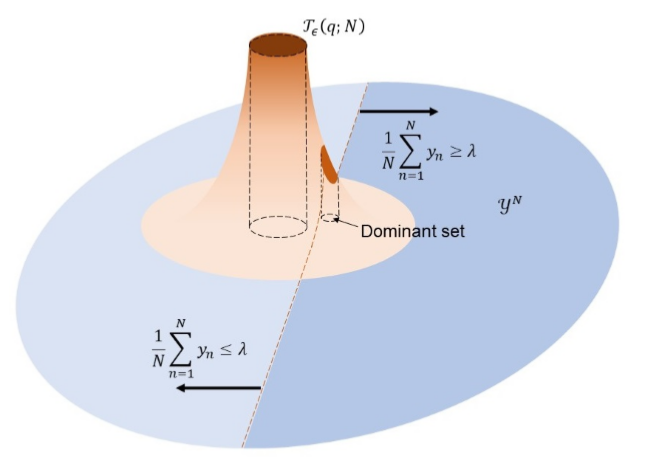
Theorem (Cram´er’s Theorem): \(\vec{\boldsymbol{y}}=[y_1,y_2,...,y_N]^T, \ \ \ y_i \sim q \ \ \ i.i.d\) with mean \(\mu<\infty\) and \(\gamma>\mu\) \[ \lim _{N \rightarrow \infty}-\frac{1}{N} \log \mathbb{P}\left(\frac{1}{N} \sum_{n=1}^{N} y_{n} \geq \gamma\right)=E_{C}(\gamma) \] where \(E_C(\gamma)\) is referred as Chernoff exponent \[ E_{C}(\gamma) \triangleq D(p(\cdot ; x) \| q),\ \ \ p(\cdot ; x)=q(y) e^{x y-\alpha(x)} \] and with \(x>0\) chosen such that \[ \mathbb{E}_{p(\cdot;x)}[y]=\gamma \] Proof:

1. \(\begin{aligned} \mathbb{P}\left(\frac{1}{N} \sum_{n=1}^{N} y_{n} \geq \gamma\right) &=\mathbb{P}\left(e^{x \sum_{n=1}^{N} y_{n}} \geq e^{N x \gamma}\right) \\ & \leq e^{-N x \gamma} \mathbb{E}\left[e^{x \sum_{n=1}^{N} y_{n}}\right] \\ &=e^{-N x \gamma}\left(\mathbb{E}\left[e^{x y}\right]\right)^{N} \\ & \leq e^{-N\left(x_{*} \gamma-\alpha\left(x_{*}\right)\right)} \end{aligned}\)
2. \(\varphi(x)=x\gamma-\alpha(x)\) 是凸的，最大值取在 \(\mathbb{E}_{p\left(\cdot ; x_{*}\right)}[y]=\dot{\alpha}\left(x_{*}\right)=\gamma\)
3. 可以证明 \(x_{*} \gamma-\alpha\left(x_{*}\right)=x_{*} \dot{\alpha}\left(x_{*}\right)-\alpha\left(x_{*}\right)=D\left(p\left(\cdot ; x_{*}\right) \| q\right)\)
4. 于是有 \(\mathbb{P}\left(\frac{1}{N} \sum_{n=1}^{N} y_{n} \geq \gamma\right) \leq e^{-N E_{C}(\gamma)}\)
5. 下界的证明，暂时略...

用到的两个事实：\(p(y;x)=q(y)\exp(xy-\alpha(x))\)

1. \(D(p(y;x)||q(y))\) 随着 x 单调增加
2. \(\mathbb{E}_{p(;x)}[y]\) 随着 x 单调增加

Remarks:

1. 这个定理也相当于表达了 \(\mathbb{P}\left(\frac{1}{N} \sum_{n=1}^{N} y_{n} \geq \gamma\right) \cong 2^{-N E_{\mathrm{C}}(\gamma)}\)
2. 相当于是分布 q 向由 \(\mathbb{E}[y]=\sum_{n=1}^{N} y_{n} \geq \gamma\) 所定义的一个凸集中投影，恰好投影到边界(线性分布族) \(\mathbb{E}[y]=\gamma\) 上，而 \(q\) 向线性分布族的投影恰好就是 (10) 中的指数族表达式

cramer_thm

5. Types and type classes

• Definition: \(\vec{\boldsymbol{y}}=[y_1,y_2,...,y_N]^T\) (不关心真实服从的是哪个分布)

  • type(实质上就是一个经验分布)定义为

  \[ \hat{p}(b ; \mathbf{y})=\frac{1}{N} \sum_{n=1}^{N} \mathbb{1}_{b}\left(y_{n}\right)=\frac{N_{b}(\mathbf{y})}{N} \]

  • \(\mathcal{P}_{N}^{y}\) 表示长度为 \(N\) 的序列所有可能的 types
  • type class: \(\mathcal{T}_{N}^{y}(p)=\left\{\mathbf{y} \in y^{N}: \hat{p}(\cdot ; \mathbf{y}) \equiv p(\cdot)\right\},\ \ \ p\in\mathcal{P}_{N}^{y}\)

• Exponential Rate Notation: \(f(N) \doteq 2^{N \alpha}\) \[ \lim _{N \rightarrow \infty} \frac{\log f(N)}{N}=\alpha \] Remarks: \(\alpha\) 表示了指数上面关于 \(N\) 的阶数(log、线性、二次 ...)

• Properties

  • \(\left|\mathcal{P}_{N}^{y}\right| \leq(N+1)^{|y|}\)
  • \(q^{N}(\mathbf{y})=2^{-N(D(\hat{p}(\cdot \mathbf{y}) \| q)+H(\hat{p}(\cdot ; \mathbf{y})))}\) \(p^{N}(\mathbf{y})=2^{-N H(p)} \quad \text { for } \mathbf{y} \in \mathcal{T}_{N}^{y}(p)\)
  • \(c N^{-|y|} 2^{N H(p)} \leq\left|\mathcal{T}_{N}^{y}(p)\right| \leq 2^{N H(p)}\)

• Theorem \[ c N^{-|y|} 2^{-N D(p \| q)} \leq Q\left\{\mathcal{T}_{N}^{y}(p)\right\} \leq 2^{-N D(p \| q)} \\ Q\left\{\mathcal{T}_{N}^{y}(p)\right\} \doteq 2^{-N D(p \| q)} \]

6. Large Deviation Analysis via Types

• Definition: \(\mathcal{R}=\left\{\mathbf{y} \in y^{N}: \hat{p}(\cdot ; \mathbf{y}) \in \mathcal{S} \cap \mathcal{P}_{N}^{y}\right\}\)

Sanov’s Theorem: \[ Q\left\{\mathrm{S} \cap \mathcal{P}_{N}^{y}\right\} \leq(N+1)^{|y|} 2^{-N D\left(p_{*} \| q\right)} \\ Q\left\{\mathrm{S} \cap \mathcal{P}_{N}^{y}\right\} \dot\leq 2^{-N D\left(p_{*} \| q\right)} \\ p_{*}=\underset{p \in \mathcal{S}}{\arg \min } D(p \| q) \]

7. Asymptotics of hypothesis testing

• LRT: \(L(\boldsymbol{y})=\frac{1}{N} \log \frac{p_{1}^{N}(\boldsymbol{y})}{p_{0}^{N}(\boldsymbol{y})}=\frac{1}{N} \sum_{n=1}^{N} \log \frac{p_{1}\left(y_{n}\right)}{p_{0}\left(y_{n}\right)} \frac{>}{<} \gamma\)
• \(P_{F}=\mathbb{P}_{0}\left\{\frac{1}{N} \sum_{n=1}^{N} t_{n} \geq \gamma\right\} \approx 2^{-N D\left(p^{*} \| p_{0}^{\prime}\right)}\)
• \(P_{M}=1-P_{D} \approx 2^{-N D\left(p^{*} \| p_{1}^{\prime}\right)}\)
• \(D\left(p^{*} \| p_{0}^{\prime}\right)-D\left(p^{*} \| p_{1}^{\prime}\right)=\int p^{*}(t) \log \frac{p_{1}^{\prime}(t)}{p_{0}^{\prime}(t)} \mathrm{d} t=\int p^{*}(t) t \mathrm{d} t=\mathbb{E}_{p^{*}}[\mathrm{t}]=\gamma\)

asymptotic

8.Asymptotics of parameter estimation

Strong Law of Large Numbers(SLLN): \[ \mathbb{P}\left(\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{n=1}^{N} w_{n}=\mu\right)=1 \] Central Limit Theorem(CLT): \[ \lim _{N \rightarrow \infty} \mathbb{P}\left(\frac{1}{\sqrt{N}} \sum_{n=1}^{N}\left(\frac{w_{n}-\mu}{\sigma}\right) \leq b\right)=\Phi(b) \] 以下三个强度依次递减

1. 依概率 1 收敛(SLLN)：\(\mathsf{x}_{N} \stackrel{w . p .1}{\longrightarrow} a\)

2. 概率趋于 0(WLLN):

3. 依分布收敛: \(\mathsf{x}_{N} \stackrel{d}{\longrightarrow} p\)

• Asymptotics of ML Estimation

  Theorem: \[ \hat{x}_{N}=\arg \max _{x} L_{N}(x ; \mathbf{y}) \] 在满足某些条件下(mild conditions)，有 \[ \begin{array}{c}{\hat{x}_{N} \stackrel{w \cdot p \cdot 1}{\longrightarrow} x_{0}} \\ {\sqrt{N}\left(\hat{x}_{N}-x_{0}\right) \stackrel{d}{\longrightarrow} \mathcal{N}\left(0, J_{y}\left(x_{0}\right)^{-1}\right)}\end{array} \]