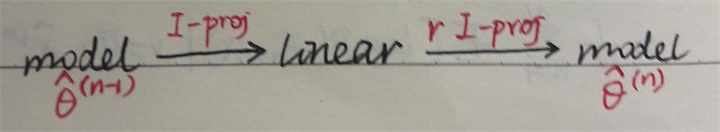统计推断(五) EM algorithm
EM 算法
1. EM-ML algorithm
- formulation
- complete data : \(\mathsf{z=[y,w]}\)
- observation : \(\boldsymbol{y}\)
- hidden variable : \(\boldsymbol{w}\)
- estimation : \(\mathcal{x}\)
- Derivation
期望获得 ML 估计,但是实际中 \(p(y;x)\) 可能很难计算(比如 mixture gaussian model,相乘后再求和) \[ \hat{x}_{ML}(y)=\arg\max_x \ln p(y;x) \\ \] 引入 complete data \(\mathsf{z=[y,w]}\),令 \(y=g(z)\) \[ p(z;x)=\sum_y p(z|y;x)p(y;x)=p(z|g(z);x)p(g(z);x) \\ \hat{x}_{ML}(y) = \arg\max_x \ln p(z;x) - \ln p(z|y;x) \] 由于 \(\hat{x}_{ML}(y)\) 与 z 无关,因此右边可以对 \(p(z|y;x')\) 求期望 \[ \begin{align} \ln p(y;x) &= \ln p(z;x) - \ln p(z|y;x) \\ &= \mathbb{E}[\ln p(z;x)|\mathsf{y}=y;x'] - \mathbb{E}[\ln p(z|y;x)|\mathsf{y}=y;x'] \\ &= U(x,x') + V(x,x') \end{align} \] 其中 \(V(x,x')\) 根据 Gibbs 不等式可以知道恒有 \(V(x,x') \ge V(x',x')\)
因此要使 \(\ln p(y;x)\) 最大,只需要使 \(U(x,x')\) 最大(可以放松要求,只要每次\(U(x,x')\)增大就可以了,这就是Generalized EM)
E-step: compute \(U(x,\hat{x}^{n-1})=\mathbb{E}[\ln p_\mathsf{z}(z;x)|\mathsf{y}=y;\hat{x}^{n-1}]\)
M-step: maximize \(\hat{x}^n = \arg\max_x U(x,\hat{x}|^{n-1})\)
EM-MAP 推导:待完成!
2. EM for linear exponential family
- derivation
指数分布 \[ p(z;x)=\exp\left(x^Tt(z)-\alpha(x)+\beta(z)\right) \\ U(x,x^n) = \mathbb{E}[\ln p(z;x)|y;x^n] \\ \] EM 算法迭代过程中每次要找 \(U(x,x')\) 的最大值点,因此有 \[ \frac{\partial}{\partial x}U(x,\hat{x}^n) \Big|_{x=\hat{x}^{n+1}} = \mathbb{E}[t(z)|y;\hat{x}^n] - \mathbb{E}[\dot{\alpha}(x)|y;\hat{x}^n] =\mathbb{E}[t(z)|y;\hat{x}^n] - \dot{\alpha}(x)|_{x=\hat{x}^{n+1}}=0 \] 同时由于 linear exponential family 本身的性质,有 \[ \mathbb{E}[t(z);\hat{x}^{n+1}] = \dot{\alpha}(x)|_{x=\hat{x}^{n+1}} \] 因此实际上每一步迭代过程中都满足 \[ \mathbb{E}[t(z);\hat{x}^{n+1}] = \mathbb{E}[t(z)|y;\hat{x}^n] \] 最终收敛于不动点 \[ \mathbb{E}[t(z);\hat{x}^{*}] = \mathbb{E}[t(z)|y;\hat{x}^*] \] 此时有 \[ \frac{\partial \ln p(y;x)}{\partial x} = ... = \mathbb{E}[t(z)|y;\hat{x}^*]-\mathbb{E}[t(z);\hat{x}^*] = 0 \]
3. Empirical ditribution
- observation: \(\boldsymbol{y}=[y_1,...,y_N]^T\)
- empirical ditribution: \(\hat{p}_\mathsf{y}(b;\boldsymbol{y}) = \frac{1}{N}\sum_n \mathbb{I}_b(y_n)\)
Porperties 1: \(\frac{1}{N}\sum_n f(y_n)=\sum_y f(y)\hat{p}_\mathsf{y}(y;\boldsymbol{y})\)
Properties 2: Let the set of models be \(\mathcal{P}=\{p_y(\cdot;x),x\in \mathcal{X}\}\), then the ML can be written as \[ \hat{x}_{ML}(y)=\arg\min_{p\in\mathcal{P}}D(\hat{p}_y(\cdot;y) || p) = \arg\min_{x\in\mathcal{X}}D(\hat{p}_y(\cdot;y) || p(\cdot;x)) \] which is the reverse I-projection
Remark:
- 这个性质表明最大似然实际上是在找与经验分布最接近(相似)的分布对应的参数
- 给定经验分布(观察)后,实际上就相当于给定了一个线性族(想一下对应的 \(t_k(y)\) 的如何表示,提示:用元素为1或0的矩阵),这个在此处适用,在后面对 \(p_z\) 的约束也适用
- 求 ML 就是在求逆投影(reverse I-proj),这对后面理解 EM 算法的 alernating projcetions 有用
4. EM-ML Alternating projections
根据 #3 中的性质2可以获得 ML 的表达式,但是该式子过于复杂,考虑
DPI(Data processing inequality): \(y=g(z)\) \[ D(p(z)||q(z)) \ge D(p(y)||q(y)) \\ "=" \iff \frac{p_z(z)}{q_z(z)} = \frac{p_y(g(z))}{q_y(g(z))}\ \ \ \ \forall z \] 因此根据(12)式要想最小化 \(D(\hat{p}_y(\cdot;\boldsymbol{y}) || p(y;x))\) 可以考虑最小化 \(D(\hat{p}_z(\cdot;\boldsymbol{z}) || p(z;x))\)
因为 \(p(y;x)\) 的表达式很可能很复杂,但是 \(p(z;x)\) 可以简化很多
即最大似然转化为最小化 \[ \min D(\hat{p}_z(\cdot;z) || p(\cdot;x)) \]
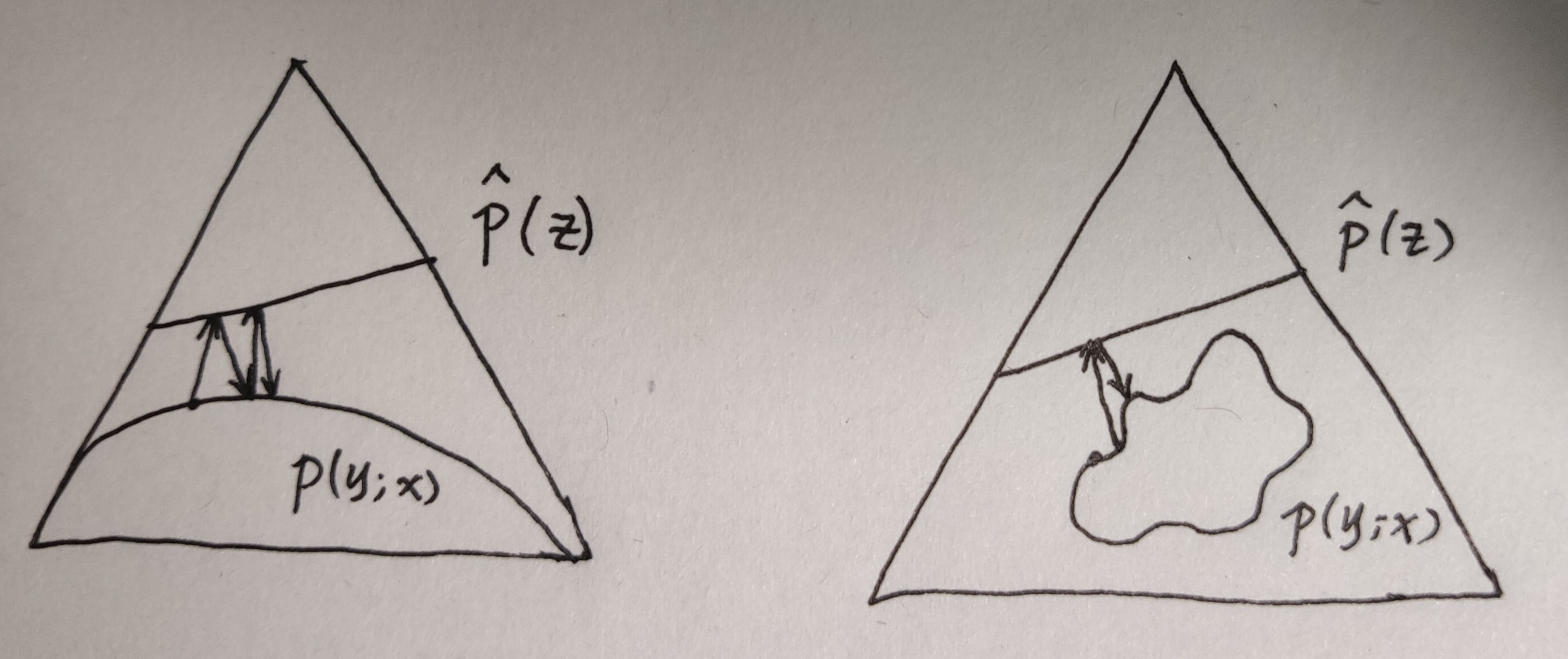
\[ \mathcal{P^Z}(y) \triangleq \left\{ \hat{p}_Z(\cdot): \sum_{g(c)=y} \hat{p}_z(c) = \hat{p}_y(b;\boldsymbol{y})\ \ \ \forall b\in \mathcal{y} \right\} \\ \]
Remarks:这里最小化过程中对两个分布都要考虑:
- 由于 \(\hat{p}_z\) 实际上在一定约束下(线性分布族,参考 #3 中的 reverse I-proj)可以任取,因此要优化 \(\hat{p}_z\) 使散度最小;
- 由于 \(p(\cdot;x)\) 实际上就是我们要求的东西(我们要找到一个 x 使观测值 y 的似然最大),因此也要优化 \(p(\cdot;x)\) 使散度最小;
要想最小化 (14) 式,可以分解为 2 步:
第一步(I-projection) \[ \hat{p}_{z}^{*}(\cdot ; \hat{x}^{(n-1)})=\underset{\hat{p}_{z} \in \hat{\mathcal{P^Z}}(\mathbf{y})}{\arg \min } D\left(\hat{p}_{z}(\cdot) \| p_{z}(\cdot ; \hat{x}^{(n-1)})\right) \]
第二步(reverse I-projection) \[ \hat{x}_{ML}^{(n)} = \underset{x}{\arg \min } D\left(\hat{p}_{z}^{*}\left(\cdot ; \hat{x}^{(n-1)}\right) \| p_{z}(\cdot ; x)\right) \]
这实际上就是 EM-ML 算法,证明如下:
上面两步分别对应 EM 中的 E-step 和 M-step
E-step: \[ \begin{align} \frac{1}{N}U(x,\hat{x}^{(n-1)}) &= \frac{1}{N}\mathbb{E}\left[\ln p(\boldsymbol{z};x)|\boldsymbol{y};\hat{x}^{(n-1)}\right] \\ &= \frac{1}{N}\sum_n \mathbb{E}\left[\ln p(z_n;x)|\boldsymbol{y};\hat{x}^{(n-1)}\right] \\ &= \frac{1}{N}\sum_n \sum_z \ln p(z;x) p\left(z|y_n;\hat{x}^{(n-1)}\right) \\ &= \sum_y \hat{p}_y(y;\boldsymbol{y}) \sum_z p\left(z|y;\hat{x}^{(n-1)}\right)\ln p(z;x) \\ &= \sum_y \hat{p}_y(y;\boldsymbol{y}) \sum_z \frac{\hat{p}^*(z;\hat{x}^{(n-1)})}{\hat{p}_y(g(z);\boldsymbol{y})} \ln p_z(z;x) \\ &= \sum_z \hat{p}^*(z;\hat{x}^{(n-1)}) \ln p_z(z;x) \\ &= -D\left(\hat{p}^*(z;\hat{x}^{(n-1)})||p(z;x)\right) - H\left(\hat{p}_Z^*(z;\hat{x}^{(n-1)})\right) \end{align} \] M-step:
Remarks:
- EM-ML 即在第二步中采用 ML 来估计 x,由于 ML 本身即与 reverse I-projection 等价,因此整体就是不断地在相互投影;
- 如果是 EM-MAP 就只需要将 M-step 中的 ML 估计换成 MAP 估计,但是由于 MAP 估计当中先验对于整个分布族会产生一个加权,计算复杂且没有闭式解
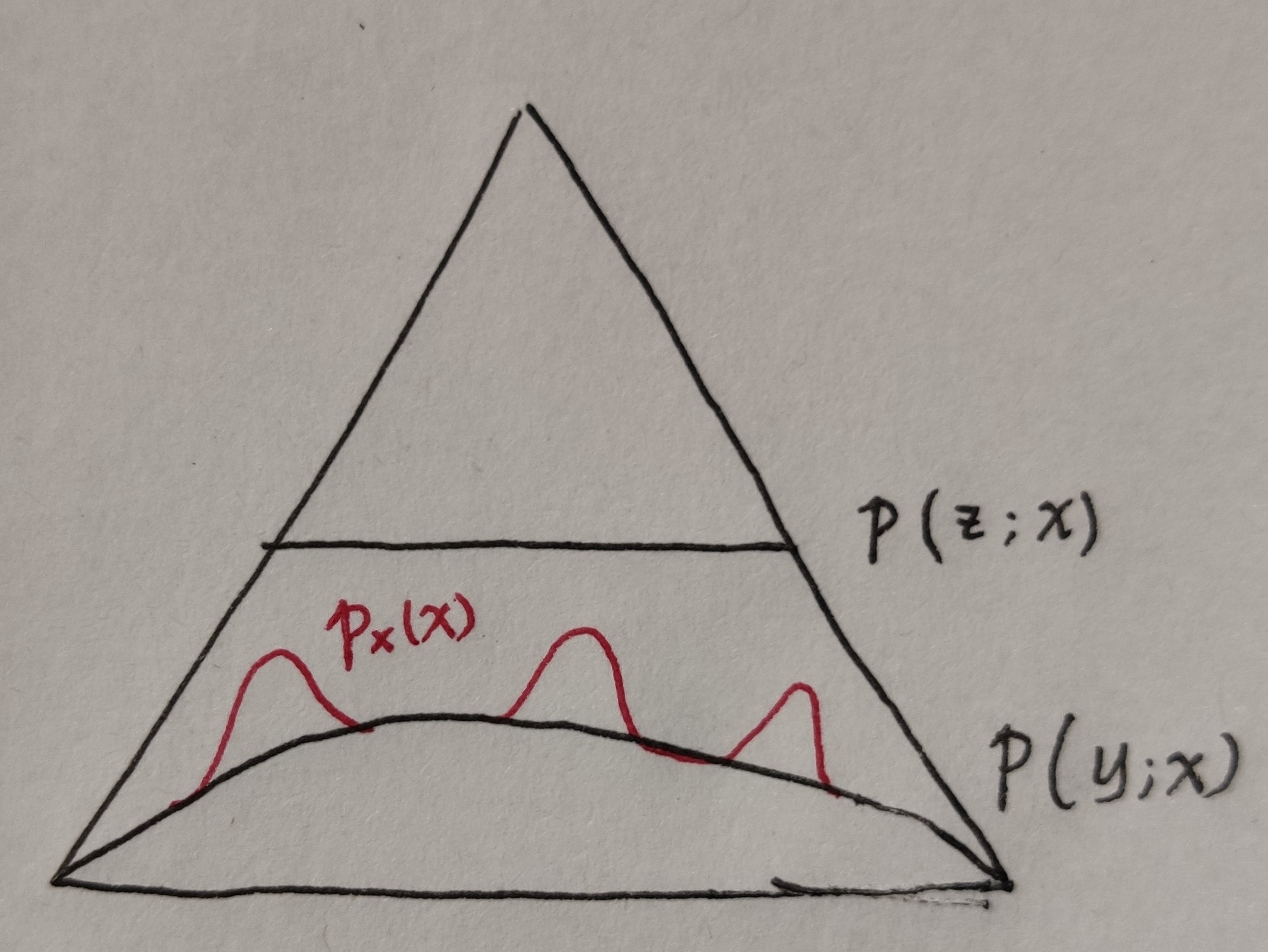
5. Remarks
EM 算法实质上可以看作一个升维的处理过。这是指将低维空间中的 \(\mathcal{Y}\) 映射到高维空间 \(\mathcal{Z}\) 中
- 根据 \(y\) 的 empirical distribution,在 \(\mathcal{P^Z}\) 中同样得到一个约束 \(z\) 的线性族
- 由预先定义的模型 \(p(z|\theta)\) 再指定另一个 \(\mathcal{P^Z}\) 中的集合,比如线性指数族
最终的目标是在 \(\mathcal{P^Z}\) 空间中获得一个最大似然估计,即 \(\hat{\theta}_{ML} = \arg\min D(\hat{p}_z || p(z,\theta))\)。 因此整个 EM 算法就是重复下面的过程