统计推断(四) Information Geometry
信息几何
1. Generalized Bayesian decision
Formulation
- Soft decision: \(q_x(\cdot|y)\)
- Cost function: \(C(x,q_x)\)
Cost function
- proper: \(p_{x|y}(\cdot|y)=\arg\min\limits_{\{q_x\ge0:\sum_a q(a)=1\}} E[C(x,q_x(\cdot))|\mathsf{y}=y]\)
- local: \(C(x,q_x)=\phi(x,q_x(x))\)
Log-loss criterion: \(C(x,q)=-A\log q_x(x) + B(x), \ \ \ A>0\)
- proper and local
Theorem: When the alphabet \(\mathcal{X}\) consists of at least 3 values (\(|\mathcal{X}| \triangleq L ≥ 3\)), then the log-loss is the only smooth local, proper cost function.
Proof: Let \(q_{l} \triangleq q_{\times}\left(x_{l}\right), p_{l} \triangleq p_{x | y}\left(x_{l} | y\right), \phi_{l}(\cdot) \triangleq \phi\left(x_{l}, \cdot\right)\)
\[ proper \Longrightarrow p_{1}, \ldots, p_{L}=\underset{\left\{q_{1}, \ldots, q_{L} \geq 0: \sum_{l=1}^{L} q_{l}=1\right\}} {\arg\min} \sum_{l=1}^{L} p_{l} \phi_{l}\left(q_{l}\right) \]
\[ 拉格朗日乘子法 \Longrightarrow p_{1}, \ldots, p_{L}=\underset{q_{1}, \ldots, q_{L}}{\arg \min } \varphi, \quad \text { with } \varphi=\sum_{l=1}^{L} p_{l} \phi_{l}\left(q_{l}\right)+\lambda\left(p_{1}, \ldots, p_{L}\right)\left[\sum_{l=1}^{L} q_{l}-1\right] \]
\[ proper \Longrightarrow \left.\frac{\partial \varphi}{\partial q_{k}}\right|_{q=p_{l}, l=1, \ldots, L}=p_{k} \dot{\phi}_{k}\left(p_{k}\right)+\lambda\left(p_{1}, \ldots, p_{L}\right)=0, \quad k=1, \ldots, L \]
由 locality 可推出 \(\lambda\) 为常数,\(\phi_k(q)=-\lambda \ln q + c_k, \ \ \ k=1,...,L\)
Gibbs inequality \[ if \ \ \ x\sim p_x(\cdot),\ \ \ \forall q(\cdot) \\ we\ \ have \ \ E_x[\log p(x)] \ge E[\log q(x)] \\ \sum_x p(x)\log p(x) \ge \sum_x p(x)\log q(x) \\ "=" \iff p(x)=q(x) \]
2. Discrete information theory
Entropy: \(H(\mathrm{x}) \triangleq \min _{q_{\mathrm{x}}} \mathbb{E}\left[C\left(\mathrm{x}, q_{\mathrm{x}}\right)\right]\)
Conditional entropy: \(H(\mathrm{x} | \mathrm{y}) \triangleq \sum_{y} p_{\mathrm{y}}(y) H(\mathrm{x} | \mathrm{y}=y)\) \(H(x | y=y) \triangleq \min _{q_{x}} \mathbb{E}\left[C\left(x, q_{x}\right) | y=y\right]\)
Mutual information: \(I(\mathrm{x} ; \mathrm{y}) \triangleq H(\mathrm{x})-H(\mathrm{x} | \mathrm{y}) = H(x)+H(y)-H(xy)\)
Conditional mutual information: \(I(\mathrm{x} ; \mathrm{y} | \mathrm{z}) \triangleq H(\mathrm{x} | \mathrm{z})-H(\mathrm{x} | \mathrm{y}, \mathrm{z})\)
Chain rule: \(I(x ; y, z)=I(x ; z)+I(x ; y | z)\)
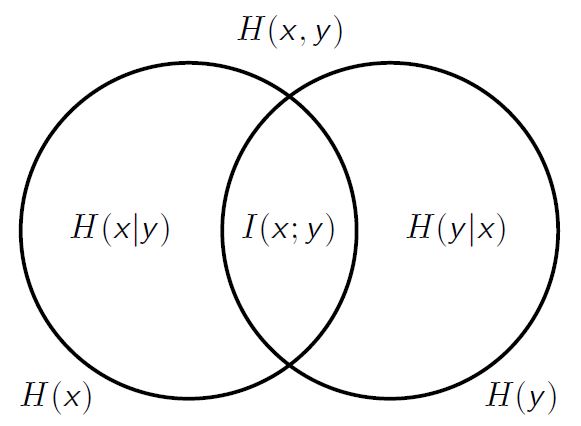
Information divergence(KL distance)
- Definition
\[ \begin{aligned} D\left(p_{\times} \| q_{\mathbf{x}}\right) & \triangleq \mathbb{E}_{p_{\mathbf{x}}}\left[-\log q_{\mathbf{x}}(\mathbf{x})\right]-\mathbb{E}_{p_{\mathbf{x}}}\left[-\log p_{\mathbf{x}}(\mathbf{x})\right] \\ &=\sum_{a} p_{\mathbf{x}}(a) \log \frac{p_{\mathbf{x}}(a)}{q_{\mathbf{x}}(a)} \end{aligned} \]
Properties
\(\ge 0\)(只有 p=q 的时候才能取 = 吗?)
\(I(x;y) = D(p_{x,y}||p_x p_y)\)
\[ \lim _{\delta \rightarrow 0} \frac{D\left(p_{y}(\cdot ; x) \| p_{y}(\cdot ; x+\delta)\right)}{\delta^{2}}=\frac{1}{2} J_{y}(x) \]
Data processing inequality (DPI)
Theorem: if \(x \leftrightarrow y \leftrightarrow t\) is a Markov chain, then \[ I(x;y) \ge I(x;t) \] with "=" \(\iff\) \(x \leftrightarrow t \leftrightarrow y\) is a Markov chain
Corollary: deterministic \(g(\cdot)\), \(I(x;y) \ge I(x;g(y))\)
Corollary: t=t(y) is sufficient \(\iff I(x;y)=I(x;t)\)
Proof: 应用互信息链式法则
Remark: 证明不等式的时候注意取等号的条件 \(I(x;y|t)=0\)
Theorem: 若 \(q_{\mathrm{x}^{\prime}}(b)=\sum_{a \in \mathcal{X}} W(b | a) p_{\mathrm{x}}(a), \quad q_{\mathrm{y}^{\prime}}(b)=\sum_{a \in \mathcal{X}} W(b | a) p_{\mathrm{y}}(a)\) 那么对任意 \(W(\cdot|\cdot)\) 有 \(D(q_{x'}||q_{y'}) \le D(p_x||p_y)\)
Proof: 待完成 ...
Theorem: 对确定性函数 \(\phi(\cdot)\),\(\mathsf{w}=\phi(\mathsf{z})\),有 \(J_{\mathsf{w}}(x)=J_{\mathsf{z}}(x)\)
Proof: 待完成 ...
3. Information geometry
Probability simplex
- 若字符集有 M 个字符,则概率单形为 M-1 维的超平面,且只位于第一象限
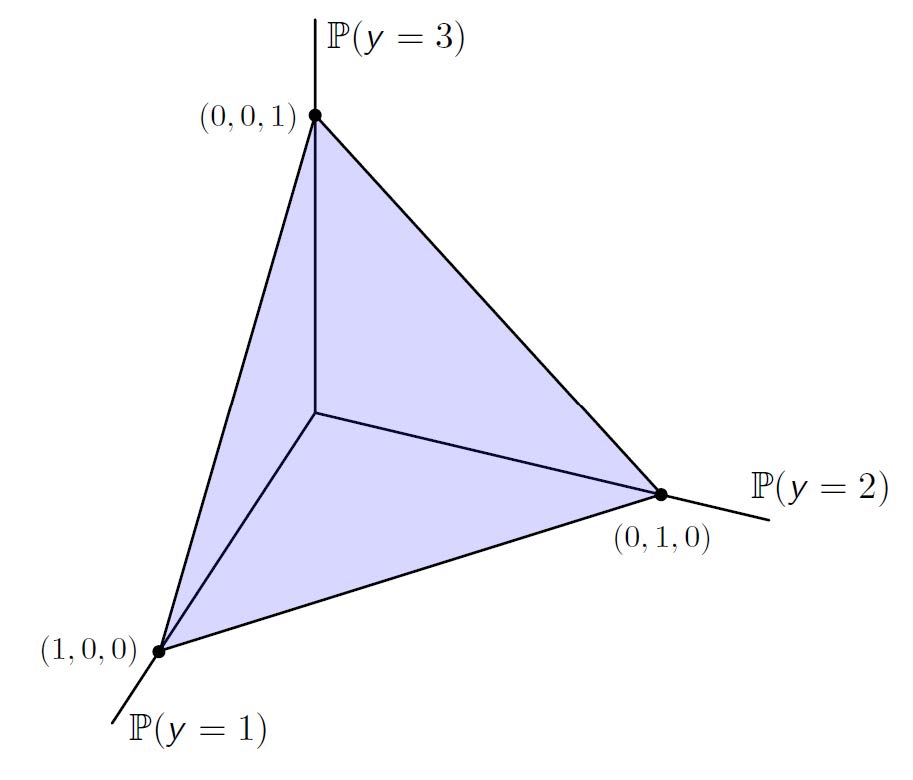
Boundary
- 根据 p,q 是否位于边界(即存在 \(p(y')=0\)) 可决定 \(D(p||q)<\infty\) 还是 \(D(p||q)=\infty\)
Local information geometry
取 \(p_0 \in \text{int}(\mathcal{P^Y})\),对任意分布(向量) \(p\) 定义其归一化表示 \[ \phi(y)=\frac{p(y)-p_0(y)}{\sqrt{2p_0(y)}} \] \(p_0\) 的邻域被定义为一个球 \[ \{p: |\phi_p(y)|\le B, \ \ \forall y \} \] 那么对小邻域内的两个分布 \(p_1,p_2\) 有 \[ D(p_1 || p_2) = \sum_y |\phi_1(y)-\phi_2(y)|^2(1+o(1)) \approx ||\phi_1-\phi_2||^2 \] 证明:代入散度公式,应用泰勒级数展开化简。其中需要注意到 \[ \sum_y \sqrt{2p_0(y)}\phi(y)=\sum_y p(y)-p_0(y) = 0 \]
Remark:直观理解就是小邻域内散度近似为欧氏距离
4. Information projection
- Definition: q 向闭集 \(\mathcal{P}\) 内的投影 \(p*=\arg\min_{p\in\mathcal{P}}D(p||q)\)
- 存在性:由于 \(D(p||q)\) 非负且对 p 连续,而 \(\mathcal{P}\) 非空且为闭集,因此一定存在
- 唯一性:不一定唯一,但如果 \(\mathcal{P}\) 为凸集,则 p* 唯一
- Pythagoras’ Theorem
Theorem(Pythagoras’ Theorem): p* 是 q 向非空闭凸集 \(\mathcal{P}\) 上的投影,那么任意 \(p\in\mathcal{P}\) 有 \[ D(p||q) \ge D(p||p^*) + D(p^*||q) \] Proof: 取 \(p_{\lambda}=\lambda p + (1-\lambda)p^* \in \mathcal{P}\)
由投影定义可知 \(\frac{\partial}{\partial \lambda} D(p_\lambda||q) \Big|_{\lambda=0} \ge 0\)
代入化简可得证
Remark: 直观理解就是不可能通过多次中间投影,使整体的KL距离(散度)减小
Corollary: 如果 q 不在 \(\mathcal{P^y}\) 的边界上,那么其在线性分布族 \(\mathcal{P}\) 上的投影 \(p^*\) 也不可能在 \(\mathcal{P^y}\) 的边界上,除非 \(\mathcal{P}\) 中的所有元素都在某个边界上
Proof: 应用散度的 Boundary、毕达哥拉斯定理
Linear families
Definition: \(\mathcal{L}\) 是一个线性分布族,如果对于一组映射函数 \(t(\cdot)=[t_1(), ..., t_K()]^T\) 和对应的常数 \(\bar t = [\bar t_1, ..., \bar t_K]^T\),有 \(\mathbb{E}_{p}\left[t_{i}(\mathrm{y})\right]=\bar{t}_{i}, \quad i=1, \ldots, K \quad\) for all \(p \in \mathcal{L}\) \[ \underbrace{\left[\begin{array}{ccc}{t_{1}(1)-\bar{t}_{1}} & {\cdots} & {t_{1}(M)-\bar{t}_{1}} \\ {\vdots} & {\ddots} & {\vdots} \\ {t_{K}(1)-\bar{t}_{K}} & {\cdots} & {t_{K}(M)-\bar{t}_{K}}\end{array}\right]}_{\triangleq \mathbf{T}}\left[\begin{array}{c}{p(1)} \\ {\vdots} \\ {p(M)}\end{array}\right]=\mathbf{0} \]
性质
- \(\mathcal{L}\) 的维度为 M-rank(T)-1
- \(\mathcal{L}\) 是一个闭集、凸集
- \(p_1,p_2 \in \mathcal{L}\),那么 \(p=\lambda p_{1}+(1-\lambda) p_{2} \in \mathcal{P}^{\mathcal{Y}}, \ \ \lambda\in R\),注意 \(\lambda\) 可以取 [0,1] 之外的数
Theorem(Pythagoras’ Identity): q 向线性分布族 \(\mathcal{L}\) 的投影 \(p^*\) 满足以下性质 \[ D(p \| q)=D\left(p \| p^{*}\right)+D\left(p^{*} \| q\right), \quad \text { for all } p \in \mathcal{L} \] Proof: 类似前面不等式的证明,只不过现在由于 \(\lambda\in R\) 所以不等号变成了等号
Theorem(Orthogonal families): \(p*\in\mathcal{P^Y}\) 为任一分布,则向线性分布族 \(\mathcal{L_t}(p^*)\) 的投影为 \(p^*\) 的所有分布都属于一个指数分布 \(\mathcal{\varepsilon}_t(p^*)\) $$ _{}(p^{}) {p ^{}: {p}[()]= {p^{}}[()]} \
\[\begin{aligned} \mathcal{E}_{\mathbf{t}}\left(p^{*}\right) \triangleq\left\{q \in \mathcal{P}^{\mathcal{Y}}: q(y)=p^{*}(y) \exp \left\{\mathbf{x}^{\mathrm{T}} \mathbf{t}(y)-\alpha(\mathbf{x})\right\}\right.\\ \text { for all }\left.y \in \mathcal{Y}, \text { some } \mathbf{x} \in \mathbb{R}^{K}\right\} \end{aligned}\]$$ 其中需要注意的是 \(\mathcal{L}_{\mathbf{t}}\left(p^{*}\right),\mathcal{E}_{\mathbf{t}}\left(p^{*}\right)\) 的表达形式并不唯一,括号内的 \(p^*\) 均可以替换为对应集合内的任意一个其他分布,他们表示的是同一个集合
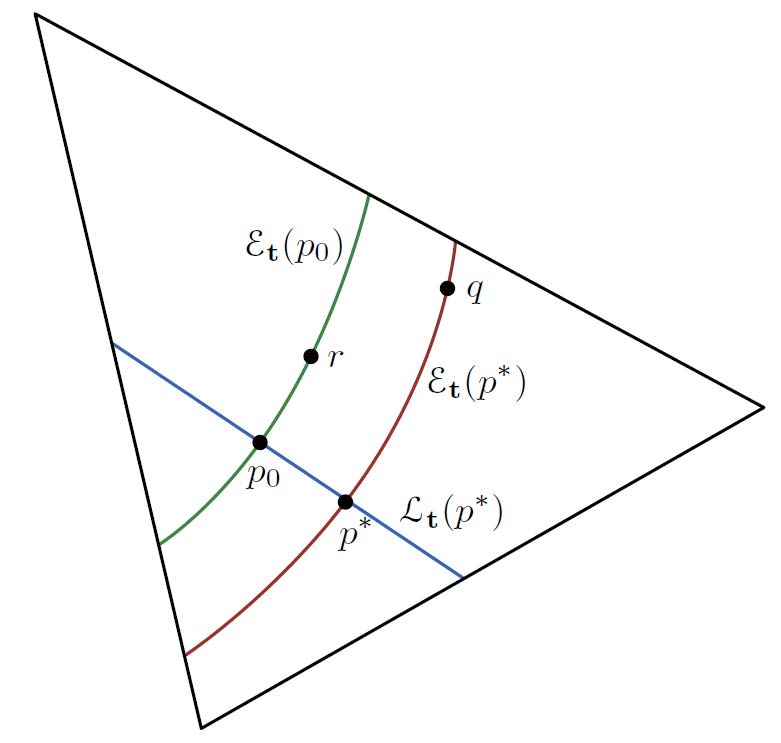
Remarks:
- 根据上面的定理,可以由 \(t(\cdot), \bar t\) 求出 q 向线性分布族的投影 p*
- 在小邻域范围内,可以发现 \(\mathcal{L}_{\mathbf{t}}\left(p^{*}\right),\mathcal{E}_{\mathbf{t}}\left(p^{*}\right)\) 的正规化表示 \(\phi_\mathcal{L}^T \phi_\mathcal{E}=0\),即二者是正交的