三维旋转、欧拉角、四元数

关于三维旋转、欧拉角和四元数，以前只是简单的调用库函数做转换，并没有深入理解，最近在网上找资料发现还是良莠不齐，很多文章写得比较杂乱，这里根据自己学习后的理解整理出一篇文章以供参考。

1. 欧拉角

欧拉角描述了三维空间中的旋转，想象有一架飞机悬在空中朝着正东方向水平静止，现在要将其姿态原地变换到任意一个其他方向，从最接近人的直观来看，在机头原始位置\(A\)和旋转后位置\(A'\)连一条线即为最短路径，沿着该最短路径旋转飞机即可。如果用数学语言描述，那么就是假设飞机中心位置为\(O\)，那么\(AOA'\)构成一个平面，以该平面法向量为轴旋转飞机，即可将飞机从原始姿态旋转到新的姿态。尽管这种方法很直观，但是一开始欧拉并没有采用这种表示方法，或许是觉得不够规整，旋转轴的确定和表示稍显麻烦。那么欧拉是如何做的呢？如下图所示^[1]，我们知道笛卡尔坐标系有\(xyz\)三个轴，那么绕着这三个轴分别做旋转不就可以了吗？这时只需要给出每次旋转的角度即可。

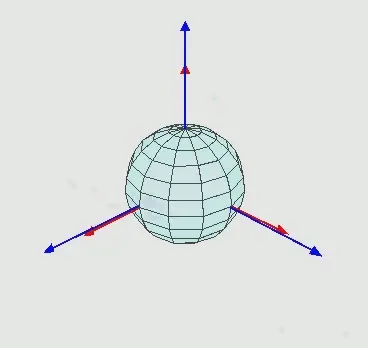
更具体清晰的描述如下：首先假设世界坐标系为\(xyz\)，飞机自身的局部坐标系为\(XYZ\)（刚体坐标系），世界坐标系始终保持固定不变，而飞机局部坐标系在飞机旋转过程中会发生变化。假设飞机初始坐标系为\(X_1Y_1Z_1(=xyz)\)，想要旋转到一个新的姿态\(X_2Y_2Z_2\)，那么欧拉给出的一个结论是：任意两个姿态之间，只需要绕 \(x,y,z(X,Y,Z)\) 轴做3次旋转即可完成。不过，具体到旋转过程中，绕哪几个轴旋转的先后顺序和角度都会对最终结果有影响^{[2]}：

内旋还是外旋：可以注意到上面动图中首先绕z轴旋转，第一次旋转之后局部坐标系的\(XY\)轴与世界坐标系的\(xy\)轴已经不对齐了，因此第二步是以局部坐标系的轴进行旋转还是以世界坐标系为轴进行旋转？前者被称为内旋，后者为外旋。显然其他参数相同的情况下，两种方式得到的结果不同。
旋转轴的顺序：欧拉角实际上有两大类，一类是Proper Euler angles，其旋转顺序包括 (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)，第二类是Tait–Bryan angles，包括 (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)。可以看到Proper Euler angles只涉及两个转轴.而Tait–Bryan angles涉及三个转轴。目前机器人以及SLAM领域中常用的是Tait–Bryan angles。后面的论述也都采用Tait–Bryan angles。
旋转的角度：指定绕 \(xyz(XYZ)\) 轴三个的旋转角度分别为 \((\alpha,\beta,\gamma)\)，需要注意的是如果旋转轴的顺序不同，即使每个轴对应的旋转角度不变，最终的姿态角也可能不同。

最后给一个小的总结，也就是说要想用欧拉角的方式描述一个三维旋转，实际上需要5个参数，即：1）内旋or外旋；2）旋转顺序；3）每次旋转的角度。

另外纠正一个重要的误解：欧拉角并不是描述一个静态的姿态角，而是描述一种过程！（相信很多人和我一样一直没意识到这点）姿态本身是唯一确定的，但是变换到这个姿态的过程是不唯一的，因此欧拉角与内旋/外旋、旋转顺序都密切相关！

2. 旋转矩阵

我们知道旋转可以用矩阵表示，如果考虑外旋的话，那么假设某个点在世界坐标系中的初始位置为 \(\boldsymbol{p}_0\)，如果跟随世界坐标系按照某个Tait–Bryan angles做外旋，不妨设为 \(x(\alpha)\to y(\beta)\to z(\gamma)\)，其旋转后的坐标（在世界坐标系中）是可以表示为 \(\boldsymbol{p}'= \boldsymbol{R} * \boldsymbol{p}_0\)，其中 \(\boldsymbol{R}\) 为旋转矩阵，那么这个旋转矩阵可以写为 \(\boldsymbol{R}_{\rm extrinsic}=\boldsymbol{R}_z(\gamma)\boldsymbol{R}_y(\beta)\boldsymbol{R}_x(\alpha)\)，其中 \[ \begin{align} \boldsymbol{R}_x(\alpha) &= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos (\alpha) & -\sin (\alpha) \\ 0 & \sin (\alpha) & \cos (\alpha) \end{array}\right] \\ \boldsymbol{R}_y(\beta) &= \left[\begin{array}{ccc} \cos (\beta) & 0 & \sin (\beta) \\ 0 & 1 & 0 \\ -\sin (\beta) & 0 & \cos (\beta) \end{array}\right] \\ \boldsymbol{R}_z(\gamma) &= \left[\begin{array}{ccc} \cos (\gamma) & -\sin (\gamma) & 0 \\ \sin (\gamma) & \cos (\gamma) & 0 \\ 0 & 0 & 1 \end{array}\right] \end{align} \] 外旋比较简单，但内旋的旋转矩阵就比较复杂，首先给出一个结论：如果内旋操作为 \(Z(\gamma) \to Y'(\beta)\to X''(\alpha)\)，那么其对应的旋转矩阵为 \[ \boldsymbol{R}_{\rm intrinsic}=\boldsymbol{R}_{X''}(\alpha)\boldsymbol{R}_{Y'}(\beta)\boldsymbol{R}_{Z}(\gamma)=\boldsymbol{R}_z(\gamma)\boldsymbol{R}_y(\beta)\boldsymbol{R}_x(\alpha) \] 也就是和前面外旋 \(x(\alpha)\to y(\beta)\to z(\gamma)\) 的结果是完全一样的。也就是说：

每种特定顺序的外旋等价于其相反顺序的内旋，例如 \(x(\alpha)\to y(\beta)\to z(\gamma)\) 与 \(Z(\gamma) \to Y'(\beta)\to X''(\alpha)\) 的旋转是等价的。

上面 \(\boldsymbol{R}_{\rm intrinsic}\) 的表达式中，第1次旋转绕 \(Z(=z)\) 轴旋转，因此 \(\boldsymbol{R}_{Z}(\gamma)=\boldsymbol{R}_z(\gamma)\)，然而在做第2次旋转的时候，此时初始的 \(Y\) 轴已经被旋转到了 \(Y'\) 处，因此绕 \(Y'\) 轴的旋转需要根据 \(Y'\) 的方向来确定，\(\boldsymbol{R}_{Y'}(\beta)\) 表达式推导较为繁琐，而第3次旋转类似，其旋转轴变为了 \(Z''\)，表达式则更为复杂。但是经过推导，会发现他们神奇地和 \(\boldsymbol{R}_z(\gamma)\boldsymbol{R}_y(\beta)\boldsymbol{R}_x(\alpha)\) 完全等价！实际上这并不是巧合，如何理解呢？下面我将参考博客^{[7]}给出解释，稍微有点绕，不想深究细节的可以只记住上面的结论，跳过这段。

首先定义一些符号，有两个坐标系，即世界坐标系 \(W\) 和旋转后刚体坐标系 \(B\)，我们一开始只考虑单步旋转，也即 \(W\) 绕某个轴（外旋，同时也是内旋）旋转1次即为 \(B\)，刚体上有一个点 \(A\) 跟着刚体坐标系做旋转，旋转后变为点 \(A'\)。记旋转前后点 A 在世界坐标系\(W\)中的坐标为 \({}^{\rm W}\boldsymbol{p}_{A}, {}^{\rm W}\boldsymbol{p}_{A'}\)，在 \(B\) 中的坐标为 \({}^{\rm B}\boldsymbol{p}_{A'}\)。那么可以有下面两个等式：

记从 \(W\) 到 \(B\) 的旋转矩阵为 \({}^{\rm W}\boldsymbol{R}_{\rm B}\)（外旋矩阵的形式，例如如果\(W\)到\(B\)是绕着\(x\)轴旋转\(\alpha\)，那么就有\({}^{\rm W}\boldsymbol{R}_{\rm B}=\boldsymbol{R}_{x}(\alpha)\)），那么我们有 \({}^{\rm W}\boldsymbol{p}_{A'} = {}^{\rm W}\boldsymbol{R}_{\rm B} {}^{\rm W}\boldsymbol{p}_{A}\)；
另一方面，由于点 \(A\) 跟着刚体坐标系做旋转，因此其在刚体坐标系中的坐标始终保持不变，也就是说我们有 \({}^{\rm B}\boldsymbol{p}_{A'} = {}^{\rm W}\boldsymbol{p}_{A}\)；

基于以上两个等式，可以得到 \({}^{\rm W}\boldsymbol{p}_{A'} = {}^{\rm W}\boldsymbol{R}_{\rm B} {}^{\rm B}\boldsymbol{p}_{A'}\)，注意到此时发生了质的变化，我们把在同一个点两个不同坐标系中的坐标，通过旋转矩阵 \({}^{\rm W}\boldsymbol{R}_{\rm B}\) 联系在了一起！实际上，矩阵\({}^{\rm W}\boldsymbol{R}_{\rm B}\)有两种含义：1）从 \(W\) 到 \(B\) 的旋转矩阵；2）空间中的同一个点，将其在\(B\)坐标系下的坐标映射到\(W\)坐标系下坐标的过渡矩阵。

那么再思考一下，所谓的外旋实际上同时也是关于坐标系 \(W\) 的内旋！如果把世界坐标系 \(W\) 直接替换成任意一个刚体坐标系 \(C\)，那么我们就有 \({}^{\rm C}\boldsymbol{p}_{A'} = {}^{\rm C}\boldsymbol{R}_{\rm B} {}^{\rm B}\boldsymbol{p}_{A'}\)。还剩下一个问题就是，\({}^{\rm C}\boldsymbol{R}_{\rm B}\) 的表达式是什么？实际上，假如 \(C\to B\) 是绕 \(x\) 轴内旋 \(\alpha\)，那么就有 \({}^{\rm C}\boldsymbol{R}_{\rm B} = \boldsymbol{R}_{x}(\alpha)\)！（思考一下为什么~）

现在考虑多步旋转，内旋操作为 \(Z(\gamma) \to Y'(\beta)\to X''(\alpha)\)，旋转过程中的坐标系分别为 \(W\to B\to C\to D\)，某一个点 A 经过多此旋转变为 \(A\to A' \to A'' \to A'''\)，旋转前 \(A\) 的坐标为 \({}^{\rm W}\boldsymbol{p}_{A}\)，由于 \(A\) 始终跟着刚体坐标系旋转，因此其在局部坐标系中的坐标始终不变，也就是 \({}^{\rm D}\boldsymbol{p}_{A'''}={}^{\rm C}\boldsymbol{p}_{A''}={}^{\rm B}\boldsymbol{p}_{A'}={}^{\rm W}\boldsymbol{p}_{A}\)，那么可以有如下关系：

先在坐标系 \(C\) 的视角下，考虑最后一次旋转操作，有 \({}^{\rm C}\boldsymbol{p}_{A'''} = {}^{\rm C}\boldsymbol{R}_{\rm D} {}^{\rm D}\boldsymbol{p}_{A'''} = \boldsymbol{R}_{x}(\alpha) {}^{\rm D}\boldsymbol{p}_{A'''} = \boldsymbol{R}_{x}(\alpha) {}^{\rm W}\boldsymbol{p}_{A}\)；
然后在坐标系 \(B\) 的视角下，考虑倒数第二次旋转操作，有 \({}^{\rm B}\boldsymbol{p}_{A'''} = {}^{\rm B}\boldsymbol{R}_{\rm C} {}^{\rm C}\boldsymbol{p}_{A'''} = \boldsymbol{R}_{y}(\beta) {}^{\rm C}\boldsymbol{p}_{A'''} = \boldsymbol{R}_{y}(\beta)\boldsymbol{R}_{x}(\alpha) {}^{\rm W}\boldsymbol{p}_{A}\)；
接着在坐标系 \(W\) 的视角下，考虑倒数第三次旋转操作，类似的有 \({}^{\rm W}\boldsymbol{p}_{A'''} = \boldsymbol{R}_{z}(\gamma)\boldsymbol{R}_{y}(\beta)\boldsymbol{R}_{x}(\alpha) {}^{\rm W}\boldsymbol{p}_{A}\)。

因此我们就得到了内旋操作 \(Z(\gamma) \to Y'(\beta)\to X''(\alpha)\) 对应的旋转矩阵恰好就是 \(\boldsymbol{R}_z(\gamma)\boldsymbol{R}_y(\beta)\boldsymbol{R}_x(\alpha)\)，和外旋 \(x(\alpha)\to y(\beta)\to z(\gamma)\) 是完全一样的。

还有另一种解释方法，旋转矩阵为何左乘是相对固定坐标系，右乘是相对当前坐标系？ - 知乎 (zhihu.com)

3. 万向锁

提到欧拉角旋转，很多文章会谈到万向锁问题，需要注意的是：欧拉角用来表示物体的旋转状态是没有问题的，万向锁是用欧拉角表示旋转过程中的一种状态，因此其影响到的是连续运动的问题^{[3]}。另外，万向锁发生在内旋过程中，外旋过程是不会发生的。万向锁现象：假设内旋 \(Z\to Y\to X\)，初始刚体坐标系为 \(X_0Y_0Z_0\)，其与世界坐标系重合，第1次旋转的时候绕着 \(Z_0/z\) 轴旋转（任意角度）后得到新的刚体坐标系 \(X_1Y_1Z_1\)，然后第2次旋转过程中绕 \(Y_1\) 轴旋转了90°/-90°，此时第2次旋转过后的刚体坐标系 \(X_2Y_2Z_2\) 中的 \(X_2\) 轴与世界坐标系中的 \(z\) 轴是同向/反向的，那么在做第3次旋转操作的时候，理应绕着此时的 \(X_2\) 轴做旋转，但从世界坐标系来看，也就等价于绕着 \(z\) 轴旋转，也就是说第1次和第3次旋转是完全可互相替代的，换言之失去了一个旋转的自由度。其他的内旋顺序也是类似的。简而言之，内旋过程中，当第二个旋转轴旋转90°/-90°时，第三个轴的转动效果可以被第一个旋转轴替代。

通常网上文章的另一种解释思路是用万向节，也就是陀螺仪的例子，个人认为这个例子不合适。首先陀螺仪中三轴万向锁中的三个轴并不总是保持互相垂直的，外圈的轴旋转并不会带动内圈轴旋转，因此它和我们直接理解刚体坐标系的旋转根本不是一回事。那么网上广为流传的那个粒子和万向锁有什么联系呢？还是结合刚才内旋 \(Z\to Y\to X\) 的例子，以及网上流传的众多图片，下面将给出一个解释。

首先对于陀螺仪而言，可以看到其结构如下，中间是一根竖轴穿过一个盘子，而盘子处于高速旋转状态，是陀螺的转子，根据陀螺的定轴性，竖轴也就是陀螺的自转轴在惯性空间内的方向保持不变。^[4]

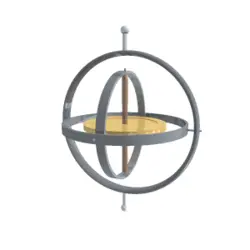
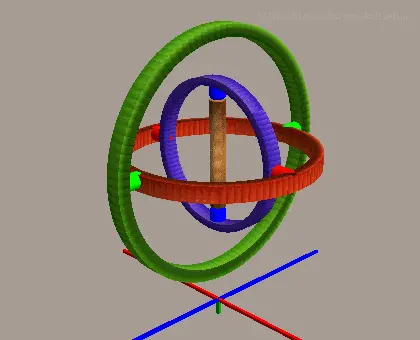
初始时刻陀螺仪的三轴对应于世界坐标系的三轴，绿色可以绕x轴旋转，红色可以绕y轴旋转，蓝色可以绕z轴旋转。

绿色绕x轴旋转	红色绕y轴旋转	蓝色绕z轴旋转

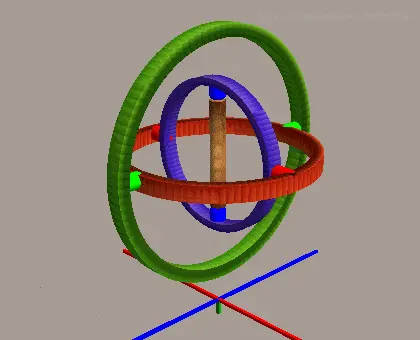第一次旋转的时候，紫色绕 \(z/Z_0\) 轴旋转，此时内圈带动外圈一起旋转，还没出什么问题；第2次旋转的时候，红色绕 \(Y_1\) 旋转，带动外圈的 \(X_1\) 也旋转，需要注意的是，经过第一次旋转之后陀螺仪的坐标轴变成了 \(X_2Y_1Z_0(=X_2Y_1z)\)，\(Z\) 轴根本没动啊！还和世界坐标系中的 \(z\) 轴保持一致；然后再第3次旋转，就只有最外层的绕 \(X_2\) 轴旋转了。对于经典配图，也就是下面这张图当中的情况而言，要达到这种状况，就是在做第2次旋转的时候使得 \(X_2\) 和 \(z\) 轴同向了，这和我们前面解释死锁问题是一致的，这两个轴同向最终导致第3次旋转的时候实际上等价于在旋转 \(z\) 轴。

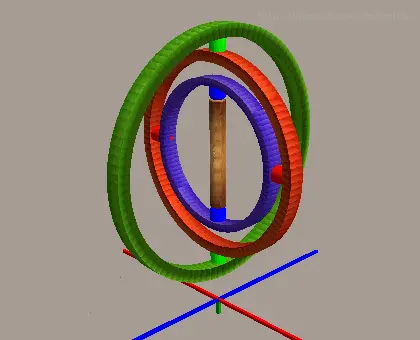
再品一下上面陀螺仪的例子，会发现刚体坐标系和世界坐标系混在一起，而且几个坐标轴还不是同等关系，很容易就把人绕进去了！害人不浅啊！因此要想理解欧拉角万向锁还是去理解前面的内旋 \(Z\to Y\to X\) 例子吧。

另一种解释思路是从矩阵运算的角度^{[5]}，考虑前面提到的旋转矩阵 \(\boldsymbol{R}=\boldsymbol{R}_x(\alpha)\boldsymbol{R}_y(\beta)\boldsymbol{R}_z(\gamma)\)，当 \(\beta=\pm\pi/2\) 的时候，会推导出 \[ \boldsymbol{R} = \left[\begin{array}{ccc} 0 & 0 & 1 \\ \sin (\alpha+\gamma) & \cos (\alpha+\gamma) & 0 \\ -\cos (\alpha+\gamma) & \sin (\alpha+\gamma) & 0 \end{array}\right] \] 这里有一点不太合适的，因为万向锁发生在内旋过程中，而这样左乘的矩阵实际上是对应的外旋操作，因此这个解释是有一点小问题的。但也说得通，因为前面提到过内旋和外旋有对应关系，所以可以认为是另一种内旋等价转换为外旋。这里可以看到复合的旋转矩阵 \(\boldsymbol{R}\) 实际上只做了2个旋转操作，也就是所谓一个自由度被“锁”住了。