信号调制与解调

写这篇文章的起因是我一直对数字调制和模拟调制这两个概念比较模糊，对于相应的通信系统结构也觉得比较混乱，所以在网上查了很多资料来理清楚这件事情。本文引用了诸多网络上的博客、文章中的文字和图片，引用之处都标注了参考出处，若有侵权请告知我，我会删除侵权部分。

信号的调制简单来说，就是用基带信号去控制（调制）单频载波信号的某个或某几个参数，从而使得调制后的信号中嵌入了希望传递的信息[1]。这个载波往往是一个高频信号，便于传输。解调则是调制的逆过程。之所以要这么做是因为：1）高频信号更容易收发传输，天线尺寸需要是波长的1/4，使用高频信号可以减小天线尺寸；2）通过调制不同频率的载波信号，可以将基带信号搬移到不同频段的载波上，便于同时传输多路不同的基带信号[2]。

1. 移动通信发展历史

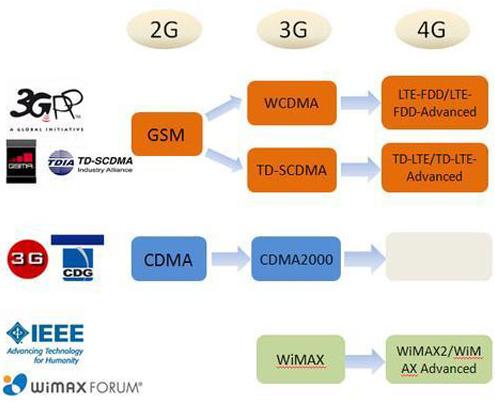
我们主要关注无线通信。移动通信最开始的目的是打电话，上世纪80年代出现了第一代（1G）移动通信网络，传输的是人的语音信号，1G使用模拟调制，多址技术为FDMA。当时使用的都是大哥大，采用模拟电路，因此手机都比较大，使用的频段在800MHz，所以天线长度大概要10cm，所以也能看到大哥大外面露出来的很长的天线，这个阶段摩托罗拉风光无限。传输速率只有2.4Kbps，要知道人的语音要想保证比较好的质量需要的速率是64Kbps，因此1G的语音通话质量也不太行[22]。

上世纪90年代，形成2G移动通信，大致可以分为两类，一类是基于TDMA的GSM标准，主要使用地区是我国和欧洲；另一类是基于CDMA的IS-95标准（也被称为cdmaOne），主要使用地区是美国。欧洲（芬兰）提出的通信标准GSM中采用了GMSK调制，而IS-95则采用QPSK和OQPSK调制，这三种都是数字调制，因此2G也将移动通信带入了数字时代。由于处理和传输的是数字信号，数字电路取代了模拟电路，能够集成在一个小小的芯片上，因此手机体积大大的减小了，诺基亚在这个阶段大杀四方。并且除了语音信号，其他的多媒体数据例如文字、图片也能传输了。GSM，工作在900MHz和1800MHz频点附近；CDMA工作在800MHz频点附近。2G移动通信，带宽有25MHz，峰值数据速率能达到14.4Kbps[20][21]。

在2G和3G中间经过了2.5G，是二者的衔接，2.5G相比于2G提供了更高的速率和更多的功能。蓝牙等技术都是2.5G技术[23]。

到3G时代，CDMA技术大行其道，作为CDMA技术的提出者，高通握着大量专利，简直是躺着赚钱。为了绕开高通的专利，欧洲日本联合起来成立了3GPP组织，提出了W-CDMA；中国搞了一个TD-SCDMA；高通与韩国组成3GPP2组织，推出了CDMA2000[24]。前两个可以看作是从GSM演化而来；CDMA2000则是从IS-95继承而来。3G的工作频段在2100MHz附近，带宽有25MHz，上行链路采用BPSK调制，下行链路采用QPSK，数据速率能达到3.1Mbps[19][20]。苹果2007年发布的iPhone也带动了3G的推广和发展。

在进入4G时代之前，插入一段关于WiFi和WiMax的历史。1999年，IEEE分别推出了802.11b与802.11a两种WiFi标准，分别使用 2.4GHz和5GHz频段，彼此标准不相容。2003 年，IEEE引入正交频分复用技术 (OFDM)，推出802.11b的改进版802.11g使传输速度从原先的11Mbps提升至54Mbps。现在我们使用的WiFi主要为802.11n， 与 802.11a、802.11b、802.11g皆兼容，并采用MIMO技术，使传输速度及距离都有所提升，速度甚至可达600Mbps[24]。

随着版图不断扩大，IT业巨头们开始觊觎起蜂窝移动通信市场大饼——4G。OFDM说起来也不是新技术，早在1960年代贝尔实验室发明OFDM后，技术框架约在1980年代便已建立完成。然而当时能支持OFDM的硬件不成熟，CDMA又由高通领军一时红火，便淘汰在3G标准之外。简单来说就是CDMA太红，如果 Intel和 IT大厂没有在WiFi上将OFDM技术发扬光大，电信业没有一家注意到早期不被重视的OFDM。由于WiMax的关系，OFDM才又重新进入电信业和学术界的视野中[24]。

2008年时，3GPP提出了长期演进技术 (Long Term Evolution, LTE) 作为3.9G技术标准。又在2011年提出了长期演进技术升级版 (LTE-Advanced) 作为4G技术标准，准备把W-CDMA汰换掉，转而采用OFDM。全球覆盖率最高的基站正是W-CDMA，因此，各大运营商无不纷纷决定采用LTE-Advanced当作第四代通信技术标准。如同高通败在W-CDMA基站的广覆盖上，LTE可兼容WCDMA，且利用现有基站配套设备，而WiMax基站却要从头建起，Intel也在2010年宣布放弃WiMax，加入LTE阵营[24]。

到4G时代，高通摆烂了，CDMA2000也没有后续向4G的演化，所以4G主要有两支，一个是从W-CDMA演化来的LTE-FDD/LTE-FDD-Advanced，另一个是从TD-SCDMA演化来的TD-LTE/TD-LTE-Advanced。4G采用的OFDM技术可以看成是多址技术，也可以看成是调制技术，实际上就是用多个相互正交的子载波同时传递多路数据，大大提高了频谱效率。FDD-LTE的工作频点在1800MHz附近，TD-LTE的工作频点在1890MHz、2350MHz、2600MHz附近，带宽有100MHz，数据速率可达100Mbps[20][26]。

Mobile communication standards

2. 调制的分类

调制信号的大致分类如下图所示[3]：

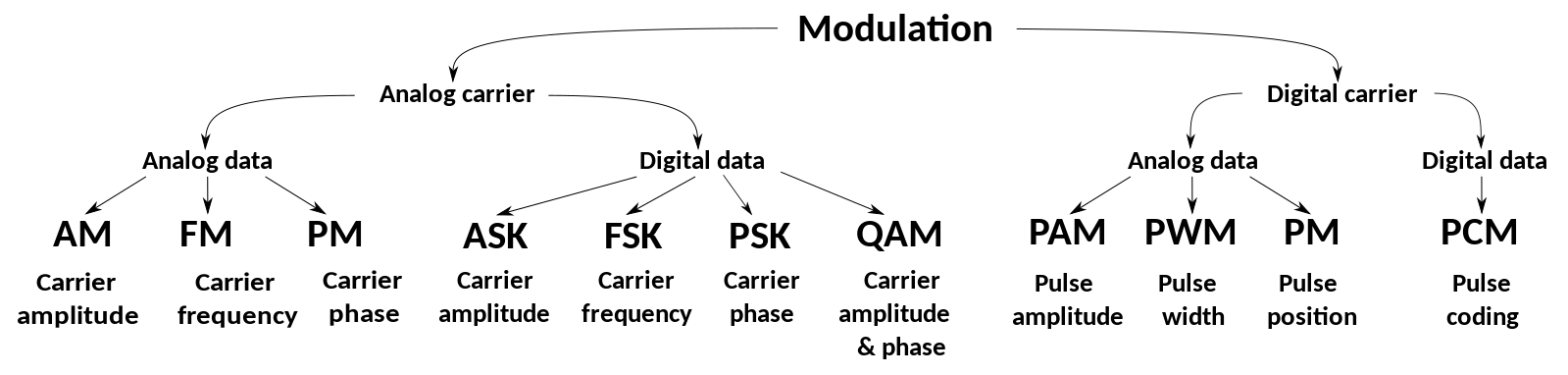
Modulation_categorization

按照载波信号（也被称为被调信号）可以分为三类：正弦波调制、脉冲调制与强度调制。调制的载波分别是正弦波，脉冲和光波。

无线通信中一般使用的载波信号都是高频正弦波，而调制过程中改变的就是正弦波的3个参数：幅度、相位、频率[1]。也就是3种基本的调制方式：调幅（AM）、调相（PM）、调频（FM）。除此之外还有一些变异的调制方法，比如正交幅度调制（QAM），单边带调幅（SM）、残留边带调幅（SSB）等[3]。 \[ {\color{red}A_c} \cos(2\pi {\color{orange}f_c} t + {\color{blue}\varphi_c}) \] 按照基带信号（也被称为调制信号）可以分为两类：模拟调制与数字调制。顾名思义，模拟调制中基带信号是模拟信号，数字调制中基带信号是数字信号。

模拟调制的中所控制的幅度、频率、相位参数是连续变化的，在解调的过程中也需要估计这个连续变化的波形；而数字调制中这些被改变的参数只是一些离散的值。模拟调制与数字调制各自的优缺点为[2]：

优点 缺点
数字调制 抗干扰能力强；
易于加密，保密性强；
便于计算机对数字信息进行处理；
便于集成化。		 需要较宽的频带；
进行数/摸转换时会带来量化误差；
要求的技术和设备复杂。
模拟调制 直观且容易实现； 保密性差，抗干扰能力差。

调制的另一种分类方法是角度调制和幅度调制，其中角度调制包括调频和调相，幅度调制包括调幅AM、双边带调制DSB、单边带调制SSB、残留边带调制VSB和正交幅度调制QAM[3]。

根据已调信号的频谱结构是否保留了原来消息信号的频谱模样，可以分为线性调制与非线性调制[5]。幅度调制一般都是线性调制，角度调制都是非线性调制。

3. 解调的分类

相干解调与非相干解调。相干解调（也被称为同步检波）适用于所有线性调制信号的解调[4]。

4. 模拟调制与解调

我们都假设基带信号是 \(m(t)\)，载波频率是 \(f_c\)，调制后的信号是 \(s(t)\)。本部分主要参考了博客[5]。

4.1 常规调幅AM

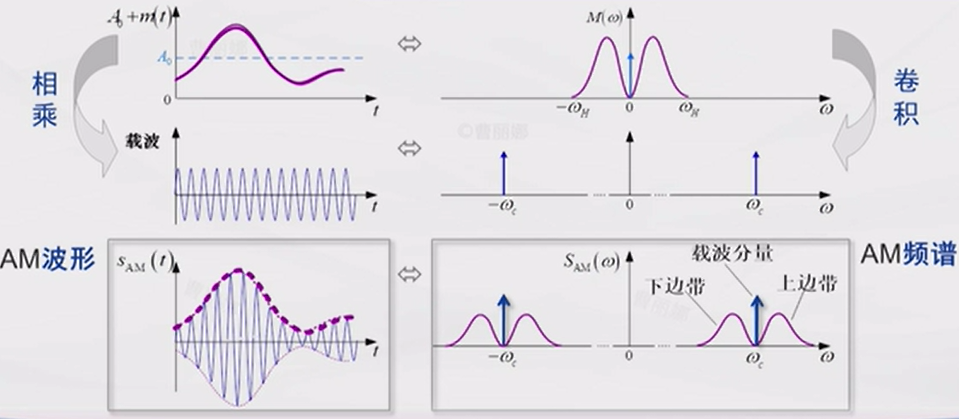
先将基带信号加上一个直流分量，然后乘以载波得到已调信号 \[ s(t) = (A_0 + m(t))\cos(2\pi f_c t) \] 对应的波形和频谱如下图所示：

AM

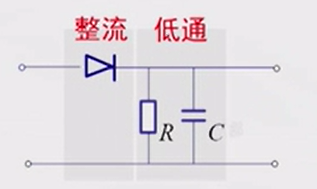
解调阶段只需要通过一个低通滤波器即可检出信号包络：

AM-demodulation

4.2 抑制载波的双边带调制DSB-SC

上面的调幅方法由于直流的存在，会导致输出的已调信号中含有载波分量\(\cos(2\pi f_c t)\)，抑制载波的双边带调制方法就是去除这个直流分量，也简称为双边带调制。 \[ s(t) = m(t) \cos(2\pi f_c t) \] DSB

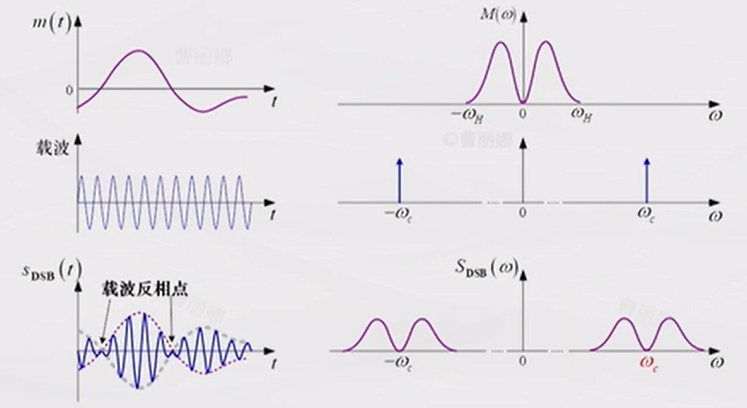
由于DSB已调信号的包络不再与基带信号\(m(t)\)成正比，因此不能使用包络检测器进行解调。通常采用的是相干解调。也就是在接收端生成一个与发送端同频同相的相关载波信号，与接收信号相乘，即可将接收信号频谱再搬到基带，通过低通滤波器后即可解调出基带信号。

调制 解调
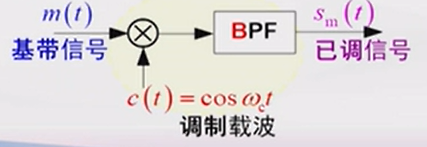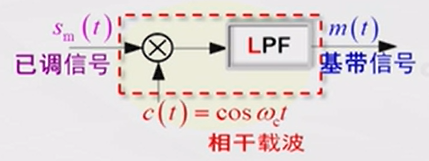系统框图 DSB-modulation DSB-demodulation
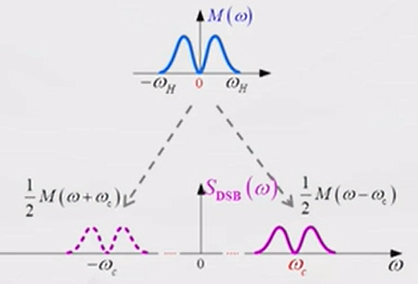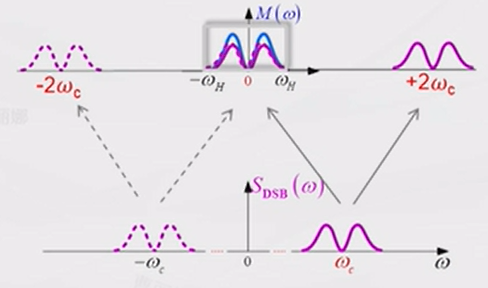频谱 DSB-modulation-spectrum DSB-demodulation-spectrum

4.3 单边带调制SSB

前面的双边带调制基带信号是对称的，搬移到载波之后实际上有一半的频谱资源是浪费掉的，没有携带有效的信息，因此单边带调制就是在DSB的基础上，要去掉一半没用的频谱，节省频谱资源。

SSB

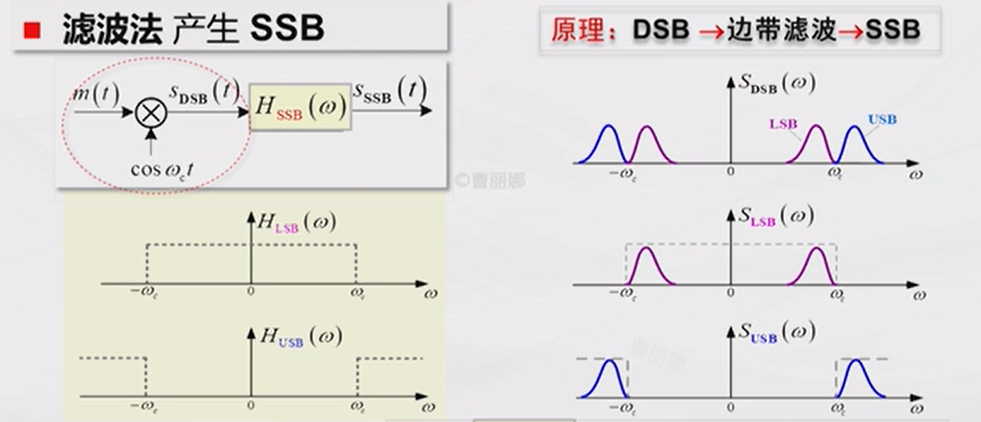
上面通过低通滤波法获得单边带已调信号对滤波器有较高的要求，需要其在载频处具有陡峭的截止特性。这难以实现，因此实际中往往是通过项移法产生SSB信号，如下图所示，推导过程可以参考博客[5]。

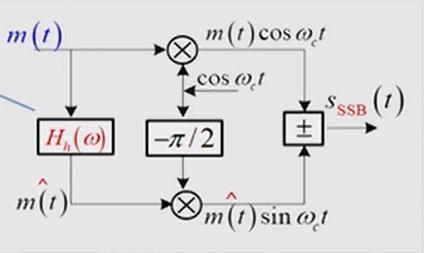
SSB-modulation

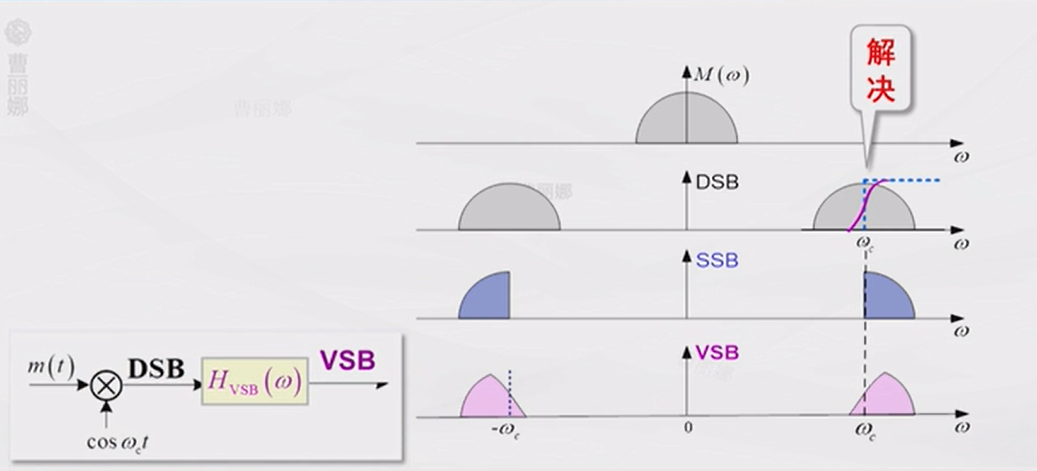
4.4 残留边带调制VSB

单边带调制需要陡峭的低通滤波器，为了解决这个问题，残留边带调制的想法虽然理想的陡峭滤波器不可实现，但是圆滑滚降的滤波器还是可以的，那就用这样的滤波器。不过这样不能将其中一半的频谱去除干净，那么是否还能够解调出基带信号呢？也是可以的，不过这个滚降滤波器的频谱需要满足一定性质，也就是在载频处具有对称性[5]。

VSB
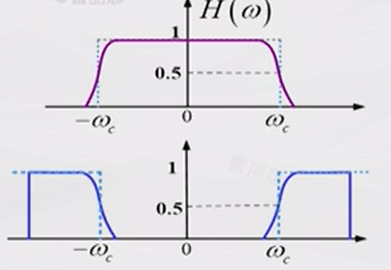
VSB-modulation-1
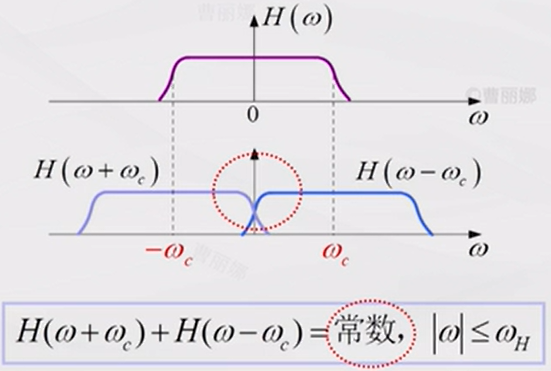
VSB-modulation-2

4.5 调相PM与调频FM

可以参考博客[6]。调频信号的包络恒定，而噪声往往是作用在信号幅度上，因此FM信号抗噪声能力强；但是FM信号需要占用较大的信号带宽，频谱利用率低。

5. 数字调制

在开始本节之前，需要明晰的一点是，相比于模拟调制，数字调制当中“调制”的概念已经被扩展了。具体而言，在模拟调制当中，基带模拟信号与高频载波通过前面介绍的几种调制方式混合之后，得到的就直接是待发送的射频信号。而在数字调制中通常包含三个阶段：

  1. 第一个阶段将二进制比特流映射为某种效率更高的数字信号（通常被称为码流），这个过程被称为基带调制；
  2. 第二个阶段将码流通过脉冲成型滤波器，将会突变的数字信号变成连续光滑的模拟信号，得到的就是基带信号；
  3. 第三个阶段将基带信号搬移到高频载波上，这个过程被称为载波调制/带通调制/射频调制。
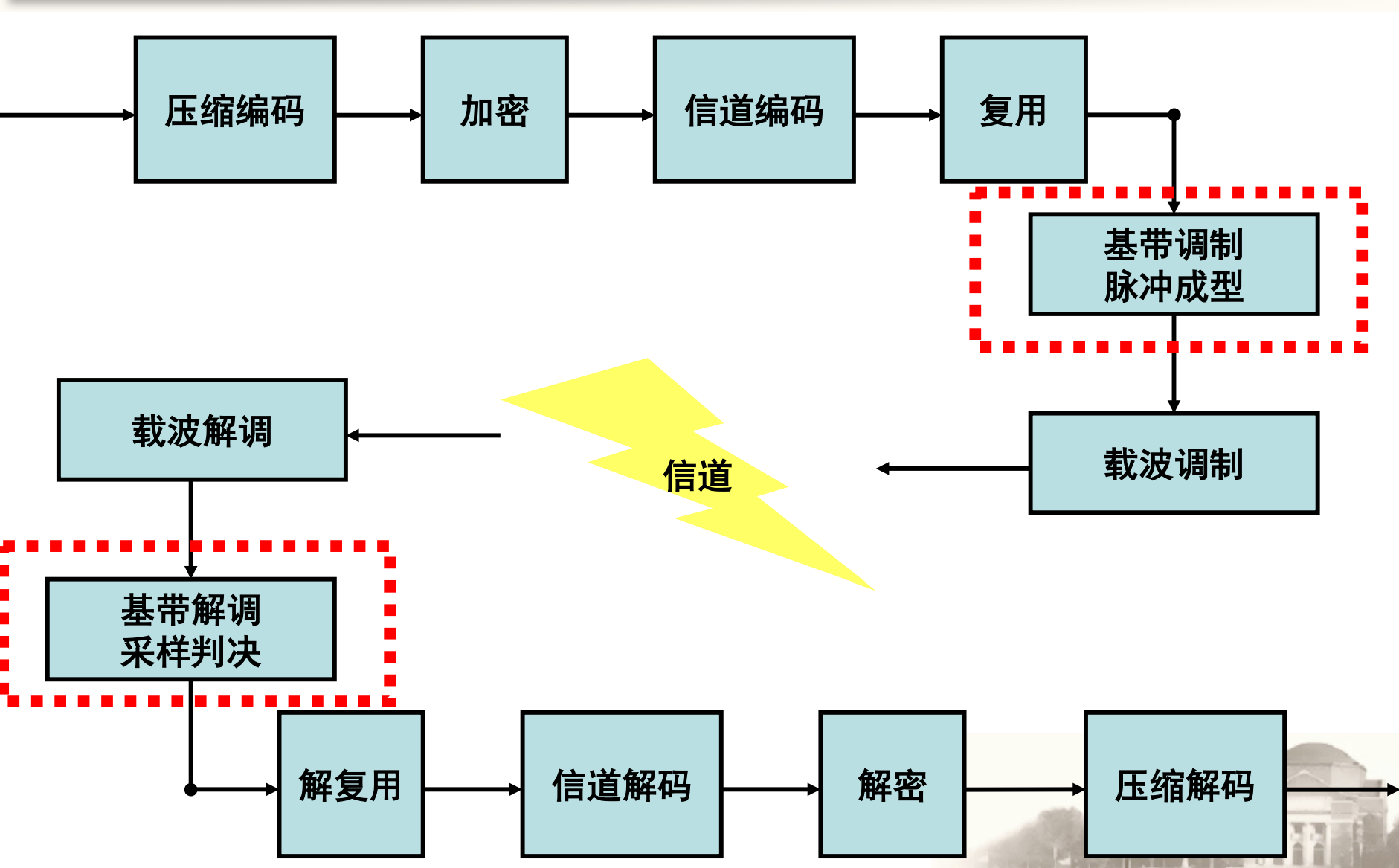
digital-communication-system-diagram

在本节的几个子小节中，5.3 IQ调制属于第三阶段载波调制，5.7脉冲成型滤波器属于第二阶段，其余的部分则属于第一阶段基带调制。为了讲述的方便以及前后逻辑的顺畅，这里将他们穿插起来，但是希望读者在脑海里能够明确他们在系统中的位置以及各自的作用。

实际上，笔者在写本文之前对模拟和数字调制感到困惑、不理解也是源于此。

5.1 二进制数字调制

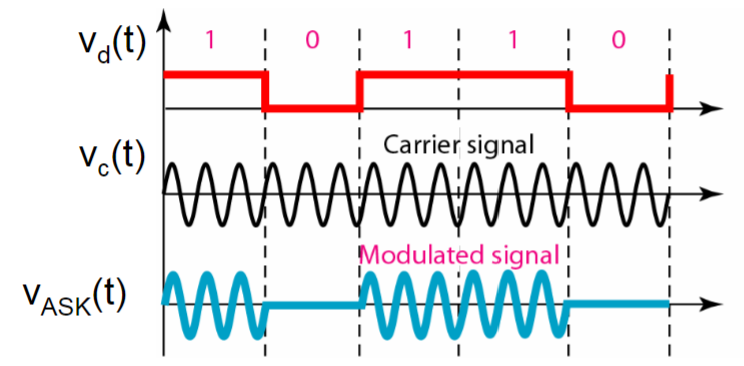
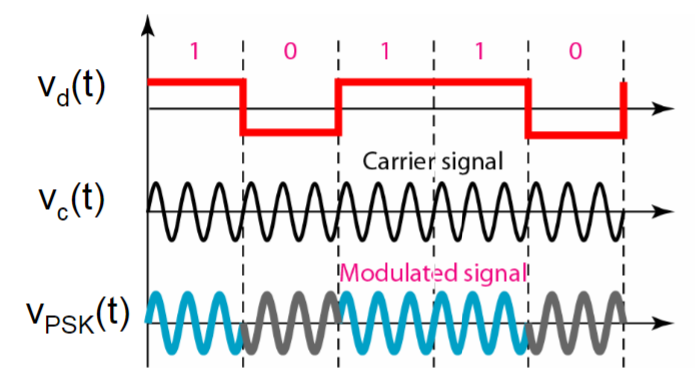
最简单的数字调制系统中，基带信号是0-1二进制数字波形，通过控制开关实现对载波的调制，因此这里面的调幅AM、调相PM、调频FM也分别被称为幅度键控ASK/通-断键控OOK、相位键控PSK、频移键控FSK。他们各自图示如下[8]：

2ASK 2PSK 2FSK
2ASK 2PSK 2FSK

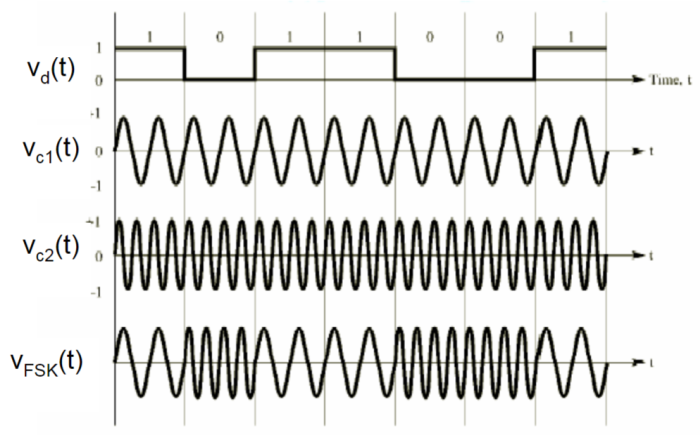5.2 多进制数字调制

二进制数字调制中，每一个符号只能表示0-1两个数值，为了提高数据传输效率，可以在一个符号内传输更多的比特，从而提高频带利用率。简单来说就是把原来的0-1比特流进行分组，例如两个bit为一组映射到一个符号（symbol、码元）上，那么一个符号就有00, 01, 11, 10这4种取值，再去调制：

  • 幅度：0，1，2，3这4个振幅；
  • 相位：0，\(\pi/2\)，\(\pi\)，\(3\pi/2\)这4个相位；
  • 频率：4个不同的载波频率。

想要传输的信号从bit流映射为了symbol流，symbol同样是只有有限个离散的取值，这个时候引入星座图会更直观更方便。什么是星座图呢？首先我们传输的正弦信号可以表示为一个复信号的实部，也就是 \[ {A_c} \cos(2\pi {f_c} t + {\varphi_c}) = \operatorname{Re}\{ {\color{blue}A_c \exp(\varphi_c)}\exp (2\pi {f_c} t)\} \] 可以看到无论是调制信号幅度还是相位，都是在单频载波\(\exp(2\pi f_c t)\)上乘以了一个复幅度\(A_c\exp(\varphi_c)\)。因此如果是幅度或者相位调制，那么我们只需要看这个复幅度就得到了想要传输的信息（symbol流）。一个复数可以映射为一个x-y二维平面上的点，那么如果我们把所有的symbol取值画出来，那么就是多个离散的点，就像是星座一样，故名星座图。BPSK（也就是2PSK）、QPSK（也就是4PSK）和8PSK示意图如下[9][16]：

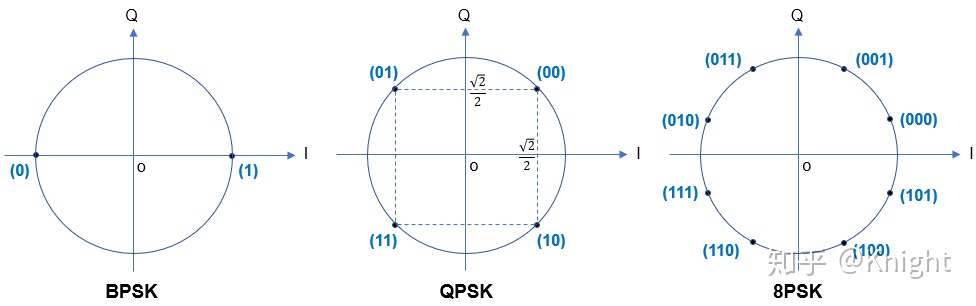
constellation-MPSK
QPSK-BPSK

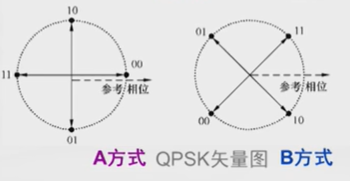
其实QPSK还有另外一种方式，就是星座图旋转45°[7]：

constellation-QPSK2

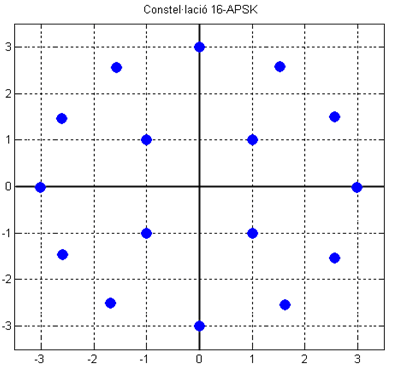
除了MPSK，幅度也是可以控制的，例如下面这个16APSK[10]：

constellation-16APSK

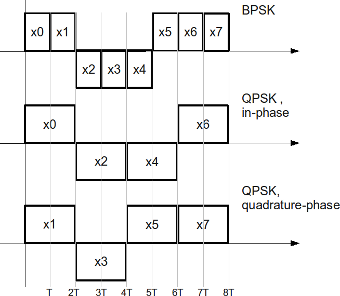
不过这里有一个问题就是：我们实际系统中只能产生实信号，而这里转换到复数域虽然看起来很简洁，但是实际系统如何实现呢？答案就是用两路信号，分别表示复信号的实部和虚部，也就是I路（In-phase）和Q路（Quadrature）。这就引出了下面的正交幅度调制QAM。

5.3 IQ调制

说白了IQ调制就是把复的基带信号搬移到高频载波上，仅此而已。前面我们已经提到了symbol可以用复数表示，那么我们要传输的码流就是一个复基带信号，记为\(s_0(t) = a(t) + j b(t)\)，其中 \(a(t)\) 和 \(b(t)\) 分别是实部和虚部，那么调制信号可以表示为 \[ s(t) = \operatorname{Re}\{s_0(t) \exp(2\pi f_c t)\} = a(t)\cos(2\pi f_c t) - b(t) \sin(2\pi f_c t) \] 在信号发射阶段，I路的基带信号就是\(a(t)\)，将其乘以\(\cos(2\pi f_ct)\)，Q路的基带信号是\(b(t)\)，将其乘以\(\sin(2\pi f_c t)\)，再将二者求和即可得到要发送的已调信号。可以参考我之前的一篇博客[11]，系统框图如下[12][13]：

IQ调制 IQ解调
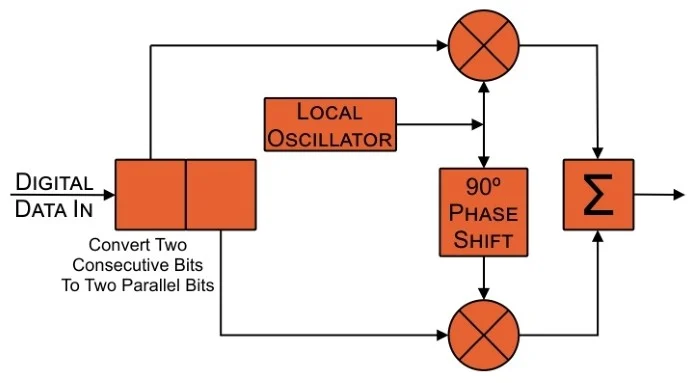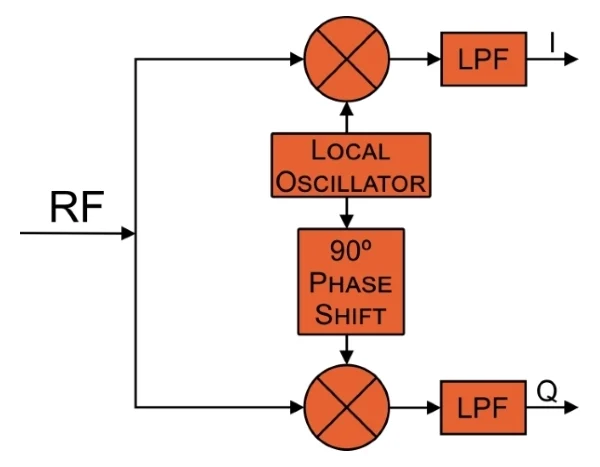diagram-IQ-modulation diagram-IQ-demodulation

IQ调制在数学上是如此的漂亮，实际系统中又是如此的方便好用，因此在现代无线通信系统中几乎是必备的。后面介绍的各种基带调制方式也基本都会配合IQ调制来使用。

5.4 正交幅度调制QAM

有了IQ调制，我们只需要分别控制I、Q两路基带信号的幅度，就能得到星座图上任意一个点，所以各种MPSK、MASK以及MAPSK等都能通过这种方式获得，这种调制方式也被称为正交幅度调制QAM。

其实也不难发现QPSK实际上就是两路（载波）相互正交的BPSK，实际上也是4QAM。

5.5 偏移四相位键控Offset-QPSK

在一般的QPSK基础上有一些变种，比如OQPSK，与QPSK的区别就在于I、Q两路的码流在时间上错开了半个码元周期，这样可以避免出现两个支路同时出现极性翻转的情况，好处是：1）避免180°的相位跳变，这种情况下最多只有90°相位跳变；2）避免I、Q两路信号同时过零点，降低信号峰均比PAR[7]。

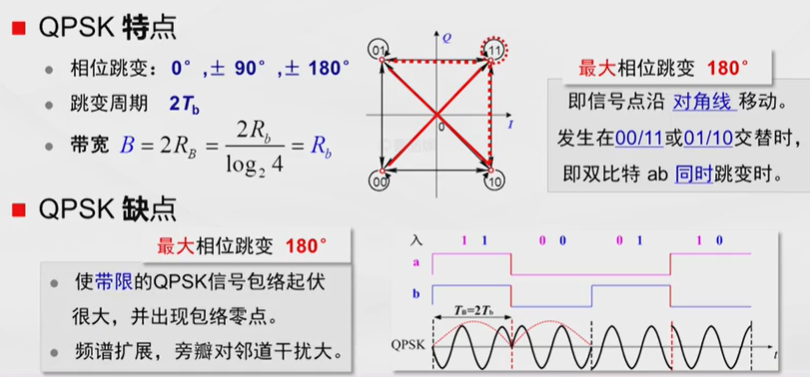
QPSK-drawback
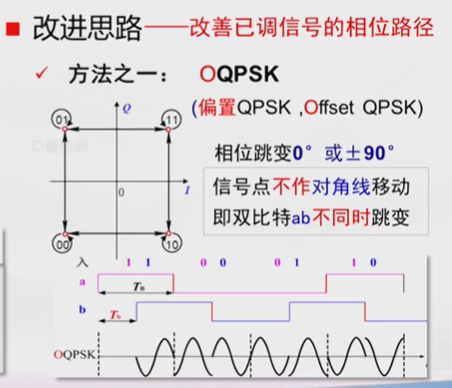
OQPSK

除此之外，还有其他的变种，例如\(\pi/4\)-QPSK等，不再赘述。

5.6 最小频移键控MSK

前面介绍的不管是二进制还是多进制，码流信号都认为是矩形波，实际上这种矩形波性能并不好。因为矩形波从时域来看会导致相位跳变，波形不光滑、不连续，从频域来看就是矩形波旁瓣幅度较大，会出现频谱扩展，对相邻信道产生干扰。为了解决这个问题，那就把矩形波换掉！换成边缘光滑的波形！

最小频移键控MSK（Minimum-shift keying）可以看成是一种特殊的OQPSK，把原来的矩形方波换成半正弦波。如果从另一个角度来看，也可以认为是频率分离为比特率二分之一的连续相位频移键控CP-BFSK（一般通过开关实现的FSK信号在边沿处也会出现波形不连续，而MSK中波形/相位总是连续的）。如下图所示[15]。

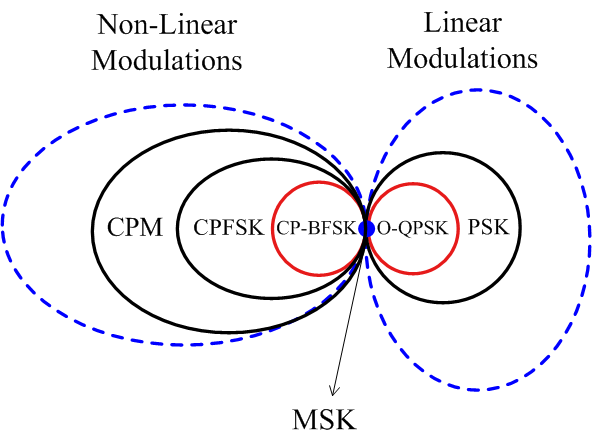
MSK-class

那么他的数学原理是什么样的呢？首先从时域来看，实际上就是将OQPSK中的矩形方波换成半正弦波，这样相邻码元的相位变化就为0。如下图所示[16][17]，一个脉冲的宽度为\(2T\)，正弦波的周期为\(4T\)。

MSK对比O-QPSK MSK的波形是连续的
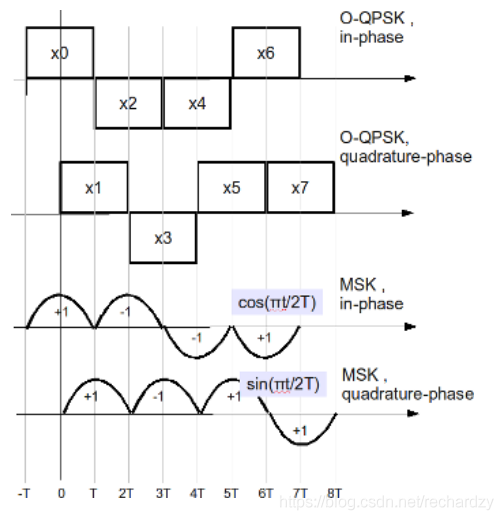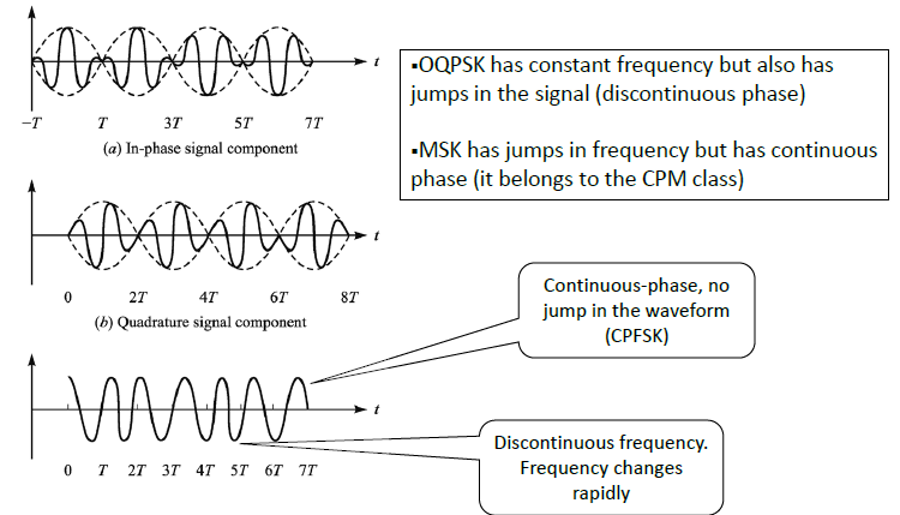MSK-OQPSK MSK-half-sin

用三角函数表示出来就是[14] \[ s(t) = a_I(t)\cos(\frac{\pi t}{2T}) \cos(2\pi f_c t) - a_Q(t)\sin(\frac{\pi t}{2T})\sin(2\pi f_c t) \] 其中\(a_I(t), a_Q(t)\)还是矩形方波，\(\cos(\pi t/2T), \sin(\pi t/ 2T)\)就是周期为\(4T\)的正弦波，一个码元周期内半个正弦波。对这个式子应用三角恒等式，就能得到 \[ \begin{aligned} s(t) &= \cos\left( 2\pi f_c t + b_k(t)\frac{\pi t}{2T} + \phi_k \right) \\ b_k(t) &= \begin{cases} 1, & a_I(t)=a_Q(t) \\ -1, & \text{others} \end{cases} \\ \phi_k &= \begin{cases} 0, & a_I(t)=1 \\ \pi, & \text{others} \end{cases} \end{aligned} \] 从频域来看，MSK是频率分离为比特率二分之一的连续相位频移键控CPFSK，也就是在一般的BFSK基础上，MSK的两个载波频率间隔恰好是码元波特率的二分之一。假设FSK的两个载波频率为\(f_1,f_2\)，码元周期为\(2T\)，由于一个码元可以传输2个比特，因此波特率为\(1/T\)，那么就有\(|f_1-f_2| = 1/2T\)。

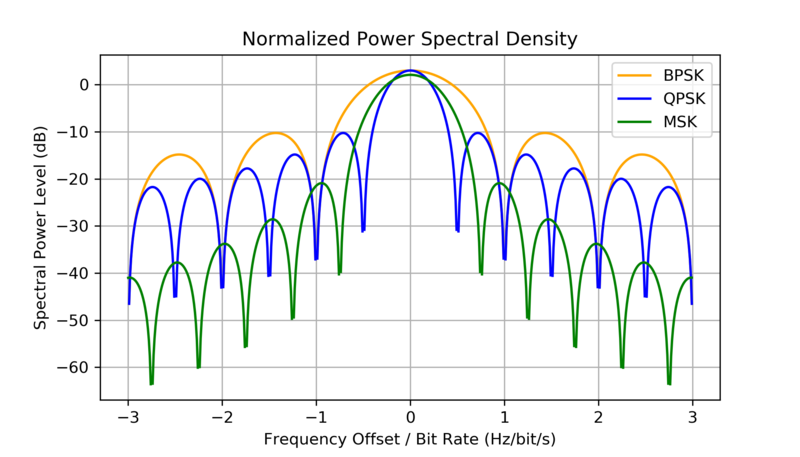
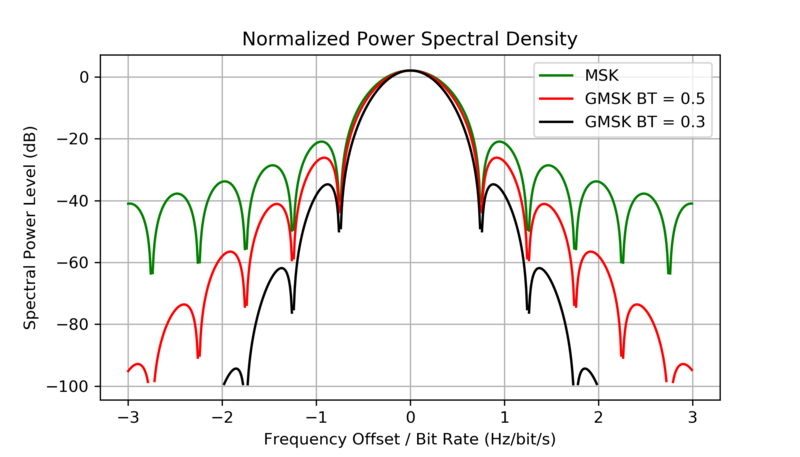
从频谱来看，MSK的旁瓣幅度相比于BPSK和QPSK也更低，因此， MSK 情况下的信道间干扰较低[14]。

MSK-spectrum

发射接收机如下图所示[16]，解调也需要相干载波。

发射机 接收机
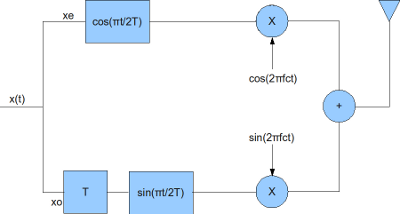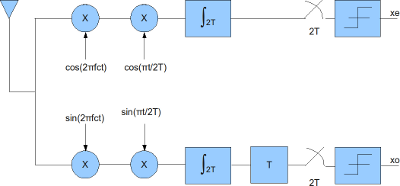MSK-modulation MSK-demodulation

5.7 脉冲成型滤波器

MSK当中将矩形波换成了半正弦波，在实现的时候直接用一个正弦波发生器加上开关就可以了，但如果我们想换成其他形状的光滑波形呢？就没有这么简单了，这里就引出了数字传输中的脉冲成型滤波器。

数字调制之后得到的码流是矩形波，从时域来看存在跳变，从频域来看频谱宽度无穷大，这在实际系统当中是不可能实现的，原因是我们无法生成跳变的信号，并且信道和收发机的通带也不是无穷带宽的。因此我们需要将码流脉冲转化为模拟信号，这个模拟信号从时域来看是连续光滑的，从频域来看是带限的，如下图所示[29]。思路很简单，将码流脉冲通过一个脉冲成型滤波器，输出信号就是滤波器冲激响应的叠加。不过关键的问题在于这个脉冲成型滤波器要怎么设计？

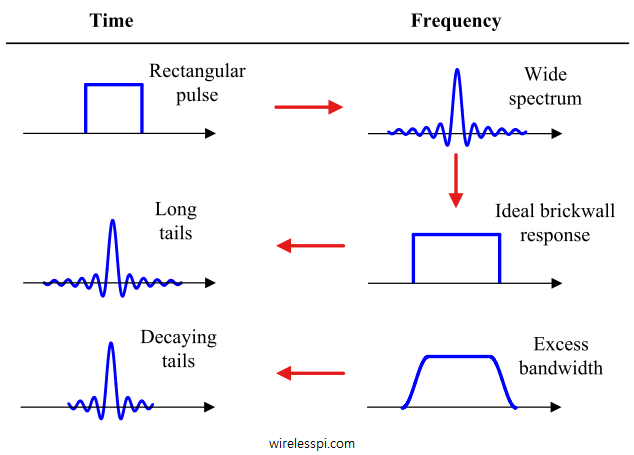
rectangular-sa

设计的关键在于不能有符号间串扰（Inter Symbol Interference, ISI）。什么意思呢？频域带限会导致时域扩展，要想当前码元对相邻的码元没有干扰，如下图所示[30]，需要其时域波形在相邻码元的采样时刻幅值为0，这就是Nyquist准则。

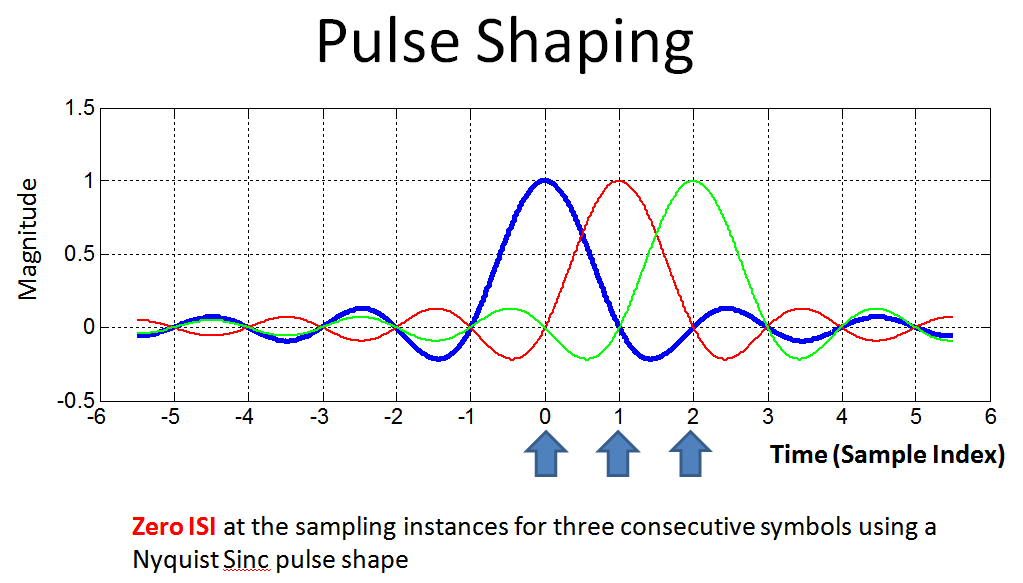
zero-ISI

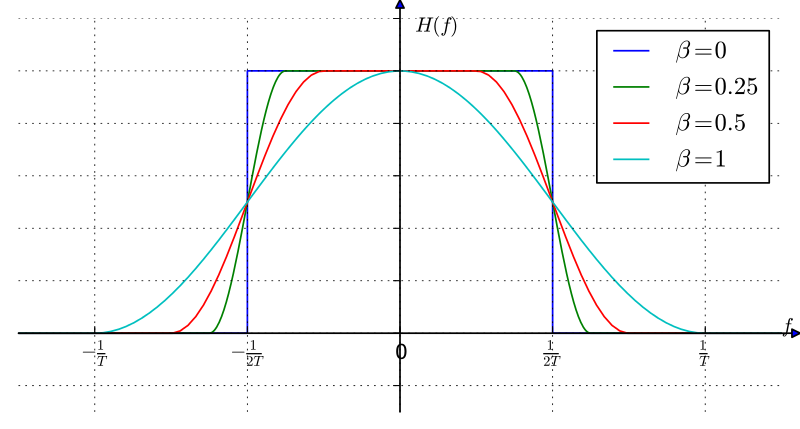
记经过基带调制的复码流为 \(\{ a_k\}\)，码元间隔（采样周期）为 \(T_s\)，脉冲成型滤波器的冲激响应为 \(g(t)\)，那么脉冲成型之后的模拟基带信号为 \[ s_0(t) = \sum_{k=-\infty}^{\infty} a_k g(t-kT_s) \] 对应的Nyquist无码间串扰条件即为： \[ g(kT_s) = \begin{cases}1, & k=0 \\ 0, & k\ne 0 \end{cases} \] 等价的频域条件为（\(G(f)\)为\(g(t)\)的傅里叶变换）[31]： \[ \frac{1}{T_s} \sum_{k=-\infty}^{\infty} G\left(f-\frac{k}{T_S}\right) = 1, \forall f \] 实际系统中常用的就是升余弦滤波器（Raised Cosine Filter），不同滚降系数的RC滤波器频谱如下图所示[31]，他两侧的边沿是余弦曲线。

raised-cosine-filter

除此之外还有Sinc filter（频谱是理想矩形），Gaussian filter（时域冲激响应是高斯的PDF）。第二代移动通信标准GSM中就采用高斯滤波器。

5.8 高斯最小频移键控GMSK

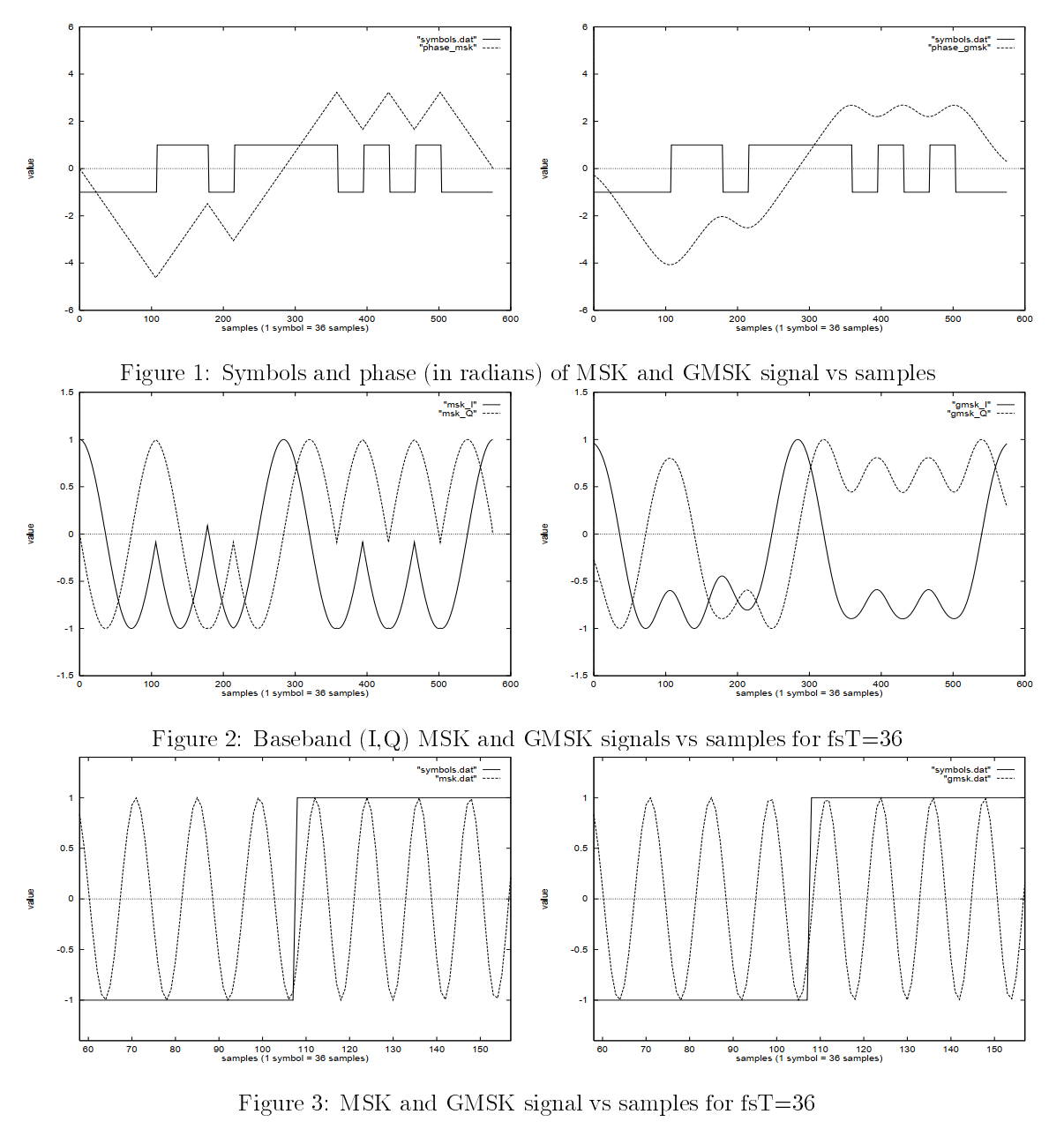
终于到了GMSK，其被应用于GSM通信标准、蓝牙、卫星通信当中。GMSK是在MSK的基础上，为了改善信号的旁瓣衰减性能，增加了一个高斯滤波器进行整形[14]。其实现方式可以是首先将基带码流通过高斯滤波器得到高斯脉冲，然后再通过MSK调制器。

GMSK-spectrum

系统框图如下所示<span class="hint--top hint--rounded" aria-label="Turletti, Thierry. "GMSK in a nutshell." Telemedia Networks and Systems Group LCS, MIT-TR(1996). ">[18]：

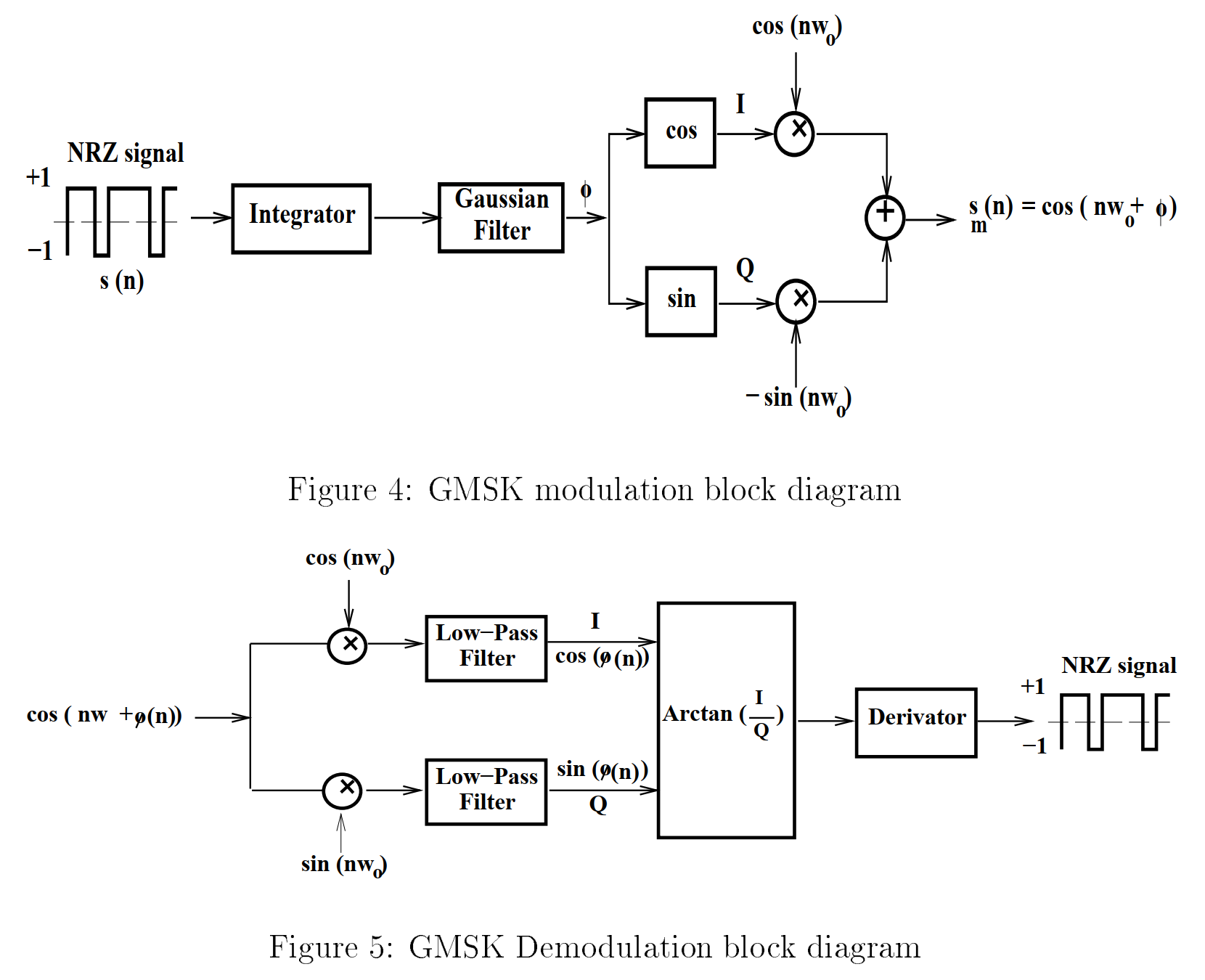
GMSK-diagram

下面的图片当中<span class="hint--top hint--rounded" aria-label="Turletti, Thierry. "GMSK in a nutshell." Telemedia Networks and Systems Group LCS, MIT-TR(1996). ">[18]，第一行是已调信号相位轨迹随着非归零码序列（-1,-1,-1,+1,+1,-1,+1,+1,+1,+1,-1,+1,-1,+1,-1,-1）的变化，可以看到GMSK输出的信号相位变化更加平缓。

GMSK-phase

5.9 正交频分复用OFDM

OFDM本身又是一个非常精妙的调制技术。简单来理解，就是同时传输多路IQ调制的信号，不同路的载波频率不同，在一个符号周期内他们相互正交，互不干扰。

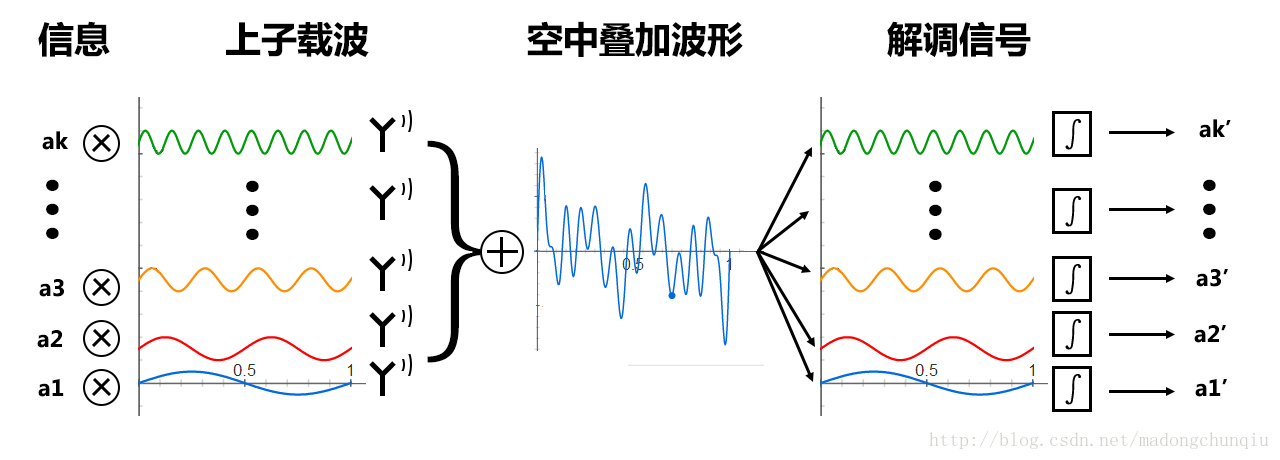
再详细一点的解释。首先对于IQ调制来说，I、Q两路本身是相互正交的，但是他们的载波还是位于同一个频点上，把两路放在一起看就是把基带信号的复频谱搬移到单一载波频点上[11]。而OFDM可以理解为在N个不同的载波频点上，并行传输了N个这样的IQ调制信号。需要注意这些子载波也不是随意选取的，需要满足在一个符号周期内的正交性，子载波之间不能有干扰。示意图如下[27]：

OFDM-parallel

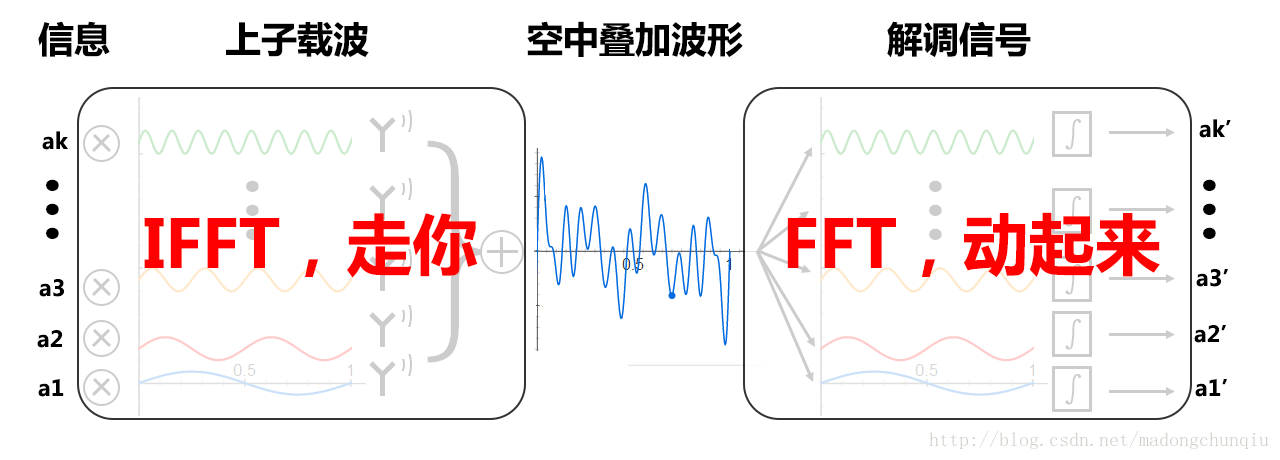
但是实际系统中直接这样实现会有很多麻烦，所以人们想出了一种非常巧妙的办法。要传输的串行二进制比特流首先转化为N路并行的比特流，每一路比特流在经过QAM映射为码流，这些码流控制了不同频点载波的复幅度，所以同一时刻不同支路的码元，实际上就是要发送信号的频谱，那么对这些系数进行IFFT，我们就把他们从频域变换到了时域，N路并行的码元映射为了1路串行的N个时刻的（复）信号，然后再将得到时域波形实部和虚部送入一个IQ调制，即可得到要发送的射频信号。示意图如下[27]：

OFDM-FFT

OFDM的系统框图如下所示[28]：

OFDM

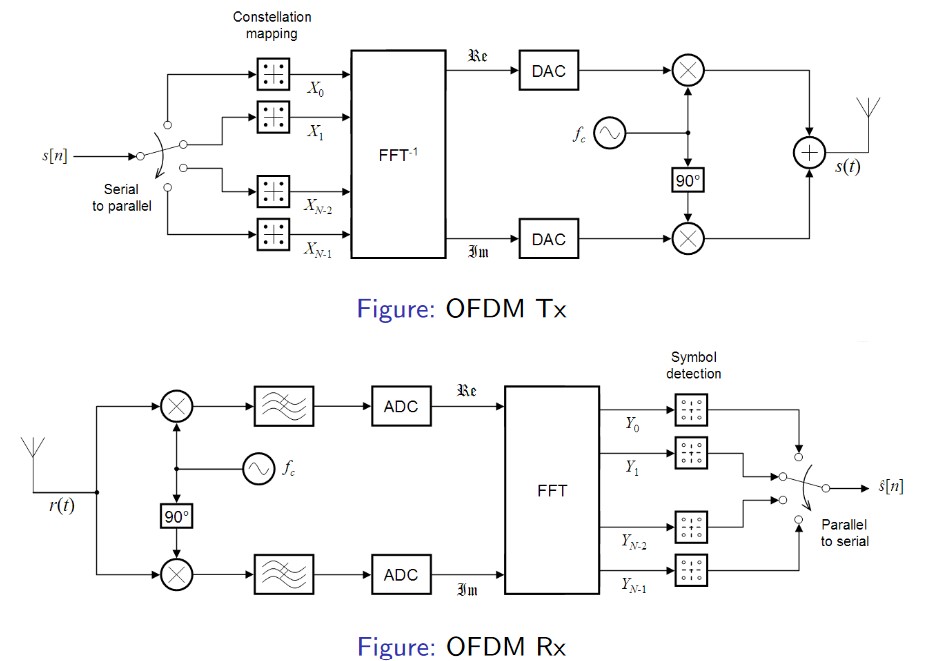
除此之外，OFDM中还包括了循环前缀以及其他细节的设计，在这里不再详细展开了，可以参考网上相关资料。LTE中OFDM采用的调制方式最高能达到256QAM，NR中能达到1024QAM[25]。

6. 数字解调

解调是调制的逆过程，所以数字解调也包括三个阶段：

  1. 第一阶段将信号从载波频段搬回到基带，如果调制的时候采用的是IQ调制，那么解调就采用IQ解调就好了；
  2. 第二阶段从模拟的基带波形中恢复出数字信号，最佳接收方案为匹配滤波并以\(1/T_s\)的频率进行采样；
  3. 第三阶段从数字信号中解调出原本想传输的比特流，需要根据星座图对得到的采样进行判决。

7. 总结

QAM和IQ调制yyds！OFDM yyds!

Reference

  1. https://www.ni.com/zh-cn/innovations/white-papers/06/analog-and-digital-modulation.html ↩︎
  2. https://blog.csdn.net/SilenceBurster/article/details/53126468 ↩︎
  3. Modulation - Wikipedia ↩︎
  4. https://blog.csdn.net/m0_51288996/article/details/121340840 ↩︎
  5. https://blog.csdn.net/weixin_50912862/article/details/114679288 ↩︎
  6. https://blog.csdn.net/weixin_50912862/article/details/114694510 ↩︎
  7. https://blog.csdn.net/weixin_50912862/article/details/114735043 ↩︎
  8. https://www.eecs.yorku.ca/course_archive/2010-11/F/3213/CSE3213_07_ShiftKeying_F2010.pdf ↩︎
  9. https://zhuanlan.zhihu.com/p/58119209 ↩︎
  10. https://en.wikipedia.org/wiki/Amplitude_and_phase-shift_keying ↩︎
  11. https://glooow1024.github.io/2021/08/29/communication/IQ-modulation/ ↩︎
  12. https://www.allaboutcircuits.com/textbook/radio-frequency-analysis-design/radio-frequency-demodulation/understanding-i-q-signals-and-quadrature-modulation/ ↩︎
  13. https://www.allaboutcircuits.com/textbook/radio-frequency-analysis-design/radio-frequency-demodulation/understanding-quadrature-demodulation/ ↩︎
  14. https://en.wikipedia.org/wiki/Minimum-shift_keying ↩︎
  15. Minimum Shift Keying (MSK) - A Tutorial - Qasim Chaudhari ↩︎
  16. http://www.dsplog.com/2009/06/16/msk-transmitter-receiver/ ↩︎
  17. https://ppt-online.org/1039280 ↩︎
  18. Turletti, Thierry. "GMSK in a nutshell." Telemedia Networks and Systems Group LCS, MIT-TR(1996). ↩︎
  19. https://en.wikipedia.org/wiki/Code-division_multiple_access ↩︎
  20. https://www.zseries.in/telecom%20lab/telecom%20generations/ ↩︎
  21. https://baike.baidu.com/item/CDMAOne/7525860 ↩︎
  22. https://blog.csdn.net/ziv669/article/details/122453973 ↩︎
  23. 2.5G_百度百科 (baidu.com) ↩︎
  24. https://blog.csdn.net/zuochao_2013/article/details/78337600 ↩︎
  25. https://blog.csdn.net/m0_52840978/article/details/123674928 ↩︎
  26. https://norstc.blog.csdn.net/article/details/80504263 ↩︎
  27. https://blog.csdn.net/madongchunqiu/article/details/18614233 ↩︎
  28. https://ecse.monash.edu/staff/eviterbo/OTFS-VTC18/Tutorial_ICC2019___OTFS_modulation.pdf ↩︎
  29. https://wirelesspi.com/pulse-shaping-filter/ ↩︎
  30. https://dsp.stackexchange.com/questions/36340/nyquist-criterion-for-zero-isi ↩︎
  31. https://en.wikipedia.org/wiki/Nyquist_ISI_criterion ↩︎
Communication and Networks
#IQ调制 #调制与解调 #移动通信 #模拟调制 #数字调制 #QAM #OFDM
信号调制与解调
https://glooow1024.github.io/2022/05/21/communication/modulation/
作者
Glooow
发布于
2022年5月21日
许可协议