【高等数值分析】Krylov子空间方法

1. 预备理论

现在需要求解一个大规模稀疏方程组 \(Ax=b\)，可以用迭代法比如 Jacobi 迭代法、Gauss-Seidel 迭代法等，不过这一节要讨论的是 Krylov 子空间方法，核心部分是 Arnoldi 迭代。

1.1 Krylov 子空间

定理（Cayley-Hamilton）：设 \(A\in{\mathbb C}^{n\times n}\)，则 \(A\) 的特征多项式 \(\chi(z)\) 是 \(A\) 的零化多项式，也即 \(\chi(A)=0\)。

假设特征多项式 \(\chi(z)=z^n + c_{n-1}z^{n-1} + \cdots + c_1 z+ c_0=(-1)^n \operatorname{det}(A)\)，那么根据 \(\chi(A)=0\) 可以得到 \[ A^{-1} = -\frac{1}{c_0} A^{n-1} - \frac{c_{n-1}}{c_0} A^{n-2} + \cdots -\frac{c_1}{c_0} I = q_{n-1}(A) \] 利用这个等式，在求解线性方程组的时候，给定任意初值 \(x_0\)，都有 \(Ax^{\ast}-Ax_0=b-Ax_0 \equiv r_0\)，于是 \(x^{\ast} = x_0 + q_{n-1}(A)r_0\)，因此理论上可以在空间 \[ \mathcal{K}=\left\{\boldsymbol{r}_{0}, A \boldsymbol{r}_{0}, \cdots, A^{m} \boldsymbol{r}_{0}, \cdots, A^{n-1} \boldsymbol{r}_{0}\right\} \] 中找到方程组的准确解，但是科学与工程计算问题中 \(n\) 可以达到 \(10^6\) 量级，直接求解代价太高。因此希望在其一个低维子空间中搜索近似解。

定义 \(m\) 维 Krylov 子空间为 \[ \mathcal{K}_{m}=\operatorname{span}\left(\boldsymbol{r}_{0}, A \boldsymbol{r}_{0}, A^{2} \boldsymbol{r}_{0}, \cdots, A^{m-1} \boldsymbol{r}_{0}\right) \] 方程组求解问题转化为 \[ \min_{x\in x_0+{\mathcal K}_m} \Vert x^{\ast} - x\Vert. \]

1.2 最佳逼近

现在的问题就是在何种范数意义下求解问题 \(\min_{x\in x_0+{\mathcal K}_m} \Vert x^{\ast} - x\Vert\)。假设 \({\mathcal K}_m\) 的一组基作为列向量构成矩阵 \(V_m\)，最优解为 \(x_m = x_0 + V_m y^{\ast} \in x_0 + {\mathcal K}_m, ~ y^{\ast}\in{\mathbb R}^{m}\)。

1.2.1 方法一：最佳平方逼近

取 \(2\) 范数 \(\min_{x\in x_0+{\mathcal K}_m} \Vert x^{\ast} - x\Vert_2\)，那么根据最佳平方逼近条件（对\(x\)求导，取零点），或者 Galerkin 正交条件，可以推出法方程为 \[ \begin{align} &\langle x^{\ast} - x_m, y \rangle = 0, ~ \forall y\in {\mathcal K}_m \\ \iff & V_m^{\rm T}(x^{\ast}-x_m) = 0 \end{align} \] 但是这个方法不可行！因为要求 \(x_m\) 就需要知道 \(x^{\ast}\)。

1.2.2 方法二：假设 \(A\) 对称正定

若 \(A\) 对称正定，那么可以改求解问题 \(\min_{x\in x_0+{\mathcal K}_m} \langle A(x-x^{\ast}), x-x^{\ast}\rangle\)，根据Galerkin 正交条件有法方程 \[ \begin{align} &\langle A(x^{\ast} - x_m), y \rangle = 0, ~ \forall y\in {\mathcal K}_m \\ \iff & r_m = A(x^{\ast}-x_m) \perp {\mathcal K}_m \\ \iff & V_m^{\rm T}(r_0 - Ax_m) = 0 \end{align} \] 这个方法可行！后面需要做两件事情：1）求出一组基 \(V_m\)；2）解法方程。

Note：这里为了得到法方程，需要假设 \(A\) 对称正定。但是在后面的 FOM 方法中，不论 \(A\) 是否正定，都基于 Galerkin 条件直接采用了这一法方程来求解线性方程组。至于这么做是否有理论支持我也不太清楚，就姑且相信它是合理的。

1.2.3 方法三：残差2范数

当 \(A\) 非奇异，不去求解 \(\min \Vert x^{\ast} - x\Vert\)，而是求解 \(\min_{x\in x_0+{\mathcal K}_m} \Vert A(x^{\ast} - x)\Vert_2\)，那么再次根据 Galerkin 条件，可以导出法方程 \[ \begin{align} &\langle A(x^{\ast} - x_m), Ay \rangle = 0, ~ \forall y\in {\mathcal K}_m \\ \iff & r_m = A(x^{\ast}-x_m) \perp A{\mathcal K}_m \\ \iff & V_m^{\rm T}A^{\rm T}(r_0 - Ax_m) = 0 \end{align} \] 这个方法也是可行的。

不论如何，上面几种方法最后都归结为两个问题：

1. 获得 \({\mathcal K}_m\) 的基底 \(V_m\)：Gram-Schmidt 正交化方法；
2. 求解法方程，并且计算残差：低维线性方程组求解。

2. 基底正交化

获得正交基底的方法主要有 Arnoldi 过程（CGS）、改进 Arnoldi 过程（MGS）、以及 Lanczos 过程。名字起的很 fancy，别被吓到，其实他们都只是 Gram-Schmidt 正交化方法。

2.1 Arnoldi 过程（CGS）

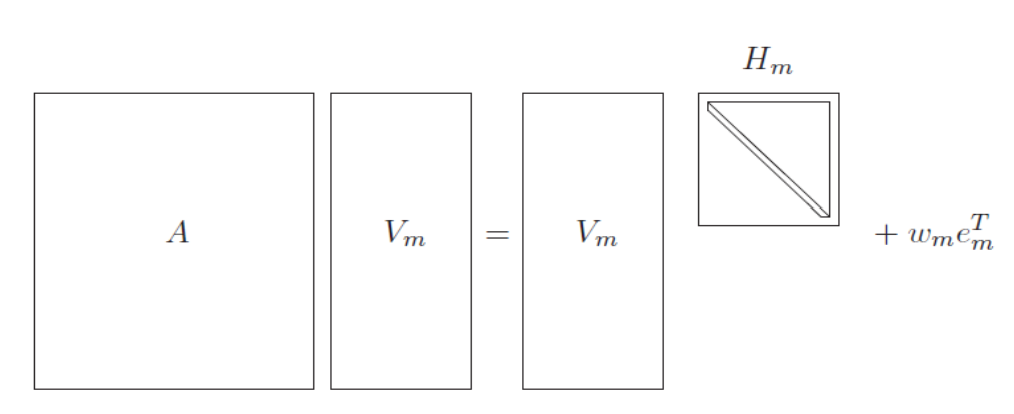
迭代过程可以归结为 \[ \begin{aligned} \boldsymbol{v}_{1} &= \boldsymbol{r}_{0} / \Vert \boldsymbol{r}_{0} \Vert \\ \boldsymbol{w}_{j} &=A \boldsymbol{v}_{j}-\langle A \boldsymbol{v}_{j}, \boldsymbol{v}_{1}\rangle \boldsymbol{v}_{1}-\langle A \boldsymbol{v}_{j}, \boldsymbol{v}_{2}\rangle \boldsymbol{v}_{2}-\cdots-\langle A \boldsymbol{v}_{j}, \boldsymbol{v}_{j}\rangle \boldsymbol{v}_{j} \\ \boldsymbol{v}_{j+1} &=\frac{\boldsymbol{w}_{j}}{\left\|\boldsymbol{w}_{j}\right\|_{2}}, j=1,2, \cdots \\ h_{i,j} &= \langle A \boldsymbol{v}_{j}, \boldsymbol{v}_{i}\rangle \end{aligned} \] 得到的 \(\{ v_1, v_2, ..., v_m,..., v_n \}\) 是单位正交基。由 \(h_{i,j}\) 作为元素构成矩阵 \(H_m \in {\mathbb R}^{m\times m}\)，可以验证 \(H_m\) 为 Hessenberg 阵，并且 \(h_{i+1,i}=\Vert \boldsymbol{w}_{i} \Vert_2\)。在 \(H_m\) 的基础上可以定义 \(\bar{H}_m \in {\mathbb R}^{(m+1)\times m}\)，也就是在最后一行下面再加一行 \([0,...,0,h_{m+1,m}]\)。

CGS-psudocode

可以验证他们满足如下等式，这三个式子在后面会频繁用到，极其重要！ \[ \begin{align} AV_m &= V_m H_m + \boldsymbol{w}_{m} \boldsymbol{e}_{m}^{\rm T} \\ &= V_{m+1} \bar{H}_m \\ V_m^{\rm T} A V_m &= H_m \end{align} \]

2.2 改进 Arnoldi 过程（MGS）

前面的 Arnoldi 过程在计算 \(\boldsymbol{w}_{j}\) 的时候，相当于把 \(A \boldsymbol{v}_{j}\) 分别计算了 \(j\) 次投影，每次都是向一个一维的子空间 \(\operatorname{span}\{ \boldsymbol{v}_{i} \}\) 投影，可能会有计算不稳定的问题。对其进行改进的方法如下，交换顺序之后，每次都是向一个 \(n-1\) 维子空间投影。

MGS-psudocode

2.3 Lanczos过程

是 Arnoldi 过程的特殊情况，当 \(A=A^{\rm T}\)，那么 \(H_m\) 为三对角矩阵，那么 \(\boldsymbol{w}_{j}\) 的计算简化为 \[ \boldsymbol{w}_{j} = A \boldsymbol{v}_{j}-\langle A \boldsymbol{v}_{j}, \boldsymbol{v}_{j-1}\rangle \boldsymbol{v}_{j-1}-\langle A \boldsymbol{v}_{j}, \boldsymbol{v}_{j}\rangle \boldsymbol{v}_{j} \]

3. 方程组求解

针对上面几种不同的迭代过程，可以有不同的求解方法。

3.1 全正交方法 (FOM)

FOM (Full orthogonalization method) 根据 Galerkin 条件，\(r_m\perp {\mathcal K}_m\)，根据法方程 \(V_m^{\rm T}(r_0 - AV_my)=0\)，因此有 \[ \begin{align} & r_m\perp {\mathcal K}_m \iff V_m^{\rm T}(r_0 - AV_my)=0 \Longrightarrow H_m y = \Vert r_0\Vert \boldsymbol{e}_1 \end{align} \] 伪代码为

FOM

根据 \(x_m = x_0 + V_m y\)，残差有 \(r_m = r_0-AV_my=r_0-(V_m H_m + \boldsymbol{w}_{m} \boldsymbol{e}_{m}^{\rm T})y = -\boldsymbol{w}_{m} \boldsymbol{e}_{m}^{\rm T} y\)。

3.2 D-Lanczos方法

若 \(A\) 对称，那么 \(H_m\) 为三对角阵，特别地记为 \(T_m\) \[ T_{m}=\left(\begin{array}{ccccc} \alpha_{1} & \beta_{2} & & & \\ \beta_{2} & \alpha_{2} & \beta_{3} & & \\ & \ddots & \ddots & \ddots & \\ & & \beta_{m-1} & \alpha_{m-1} & \beta_{m} \\ & & & \beta_{m} & \alpha_{m} \end{array}\right) \in \mathbb{R}^{m \times m} \] 记 \(T_m\) 的 LU 分解为 \[ T_{m}=L_{m} U_{m}=\left(\begin{array}{ccccc} 1 & & & & \\ \lambda_{2} & 1 & & & \\ & \ddots & \ddots & & \\ & & \lambda_{m-1} & 1 & \\ & & & \lambda_{m} & 1 \end{array}\right)\left(\begin{array}{ccccc} \eta_{1} & \omega_{2} & & & \\ & \eta_{2} & \omega_{3} & & \\ & & \ddots & \ddots & \\ & & & \eta_{m-1} & \omega_{m} \\ & & & & \eta_{m} \end{array}\right) \] 其中 \(\omega_{m}=\beta_{m}\), \(\quad \lambda_{m}=\frac{\beta_{m}}{\eta_{m-1}}\), \(\quad \eta_{m}=\alpha_{m}-\lambda_{m} \omega_{m}\)。那么根据下面这一性质，Lanczos过程可以迭代进行 \[ \begin{align} L_{m}=\left(\begin{array}{c|c} L_{m-1} & \mathbf{0} \\ \hline \boldsymbol{l}_{m-1}^{T} & 1 \end{array}\right), \quad &U_{m}=\left(\begin{array}{c|c} U_{m-1} & \boldsymbol{y}_{m-1} \\ \hline \mathbf{0}^{T} & \eta_{m} \end{array}\right) \\ L_{m}^{-1} = \left(\begin{array}{c|c} L_{m-1}^{-1} & \mathbf{0} \\ \hline -\boldsymbol{l}_{m-1}^{T}L_{m-1}^{-1} & 1 \end{array}\right), \quad & U_{m}^{-1}=\left(\begin{array}{c|c} U_{m-1}^{-1} & -\frac{1}{\eta_m} U_{m-1}^{-1} \boldsymbol{y}_{m-1} \\ \hline \mathbf{0}^{T} & 1/\eta_{m} \end{array}\right) \end{align} \] 根据这个方法，还可以到处CG（共轭梯度）法的形式。

3.3 广义极小残量法（GMRES）

Generalized minimal residual method (GMRES) 实际上就是最小化参量的二范数，即 \(\min \Vert r_m \Vert_2 = \min_{x\in x_0+{\mathcal K}_m} \Vert A(x^{\ast} - x)\Vert_2\)，根据 Galerkin 条件，应有 \(r_m\perp A{\mathcal K}_m \iff V_m^{\rm T}A^{\rm T}AV_my = V_m^{\rm T}A^{\rm T}r_0, ~ y\in{\mathbb R}^m\)。

另个一思路是 \(\min\Vert r_0-AV_my\Vert = \min \Vert V_{m+1} (\Vert r_0\Vert e_1 - \bar{H}_my)\Vert = \min \Vert \Vert r_0\Vert e_1 - \bar{H}_my\Vert\)，最小二乘解 \(\bar{H}_m^{\rm T}(\bar{H}_my - \Vert r_0\Vert e_1)=0\)。

3.4 MINRES 方法

是 GMRES 的特殊情况，当 \(A=A^{\rm T}\) 的时候，\(H_m\) 为三对角阵 \(T_m\)，\(\min \Vert r_m\Vert_2 = \min \Vert \Vert r_0\Vert e_1 - T_m y \Vert\)。