正交(IQ)调制解调与希尔伯特变换
1. 复信号
首先我们为什么需要复信号?
第一是因为复信号便于数学处理,例如获得信号的包络、相位等等;
除此之外,从频域来看,实信号频谱总是共轭对称的,也就是双边带信号,这就导致有一半的频带是无用的,浪费频谱资源,因此实际通信系统中我们更希望传输单边带的复信号。
但是在实际系统中我们只能获得实信号。
2. 正交调制解调
假设我们现在要发送一个复基带信号 \(x(t)=a(t)+jb(t)\),调制以后变成 \(x(t)\exp(j2\pi f_c t)\),但是发送的时候只能发送实信号,因此我们要取实部,因此实际发送的信号为 \[ z(t) = \text{Re}\left\{ x(t)\exp(j2\pi f_c t) \right\} = a(t)\cos(2\pi f_c t) - b(t)\sin(2\pi f_c t) \] 那么在接收端,我们希望恢复原始单边带基带信号 \(x(t)\),注意这个时候不能直接乘以 \(\cos(2\pi f_c t)\) 进行频谱搬移,因为会丢失虚部,我们想要得到的是复信号,因此就需要输出两路信号,分别为实部和虚部。那么怎么做呢?那就是 \[ z(t)\cos(2\pi f_c t) \xrightarrow{\text{low pass}} a(t) \\ z(t)\sin(2\pi f_c t) \xrightarrow{\text{low pass}} b(t) \] 参考下面这个OFDM系统框图就能很容易理解了。
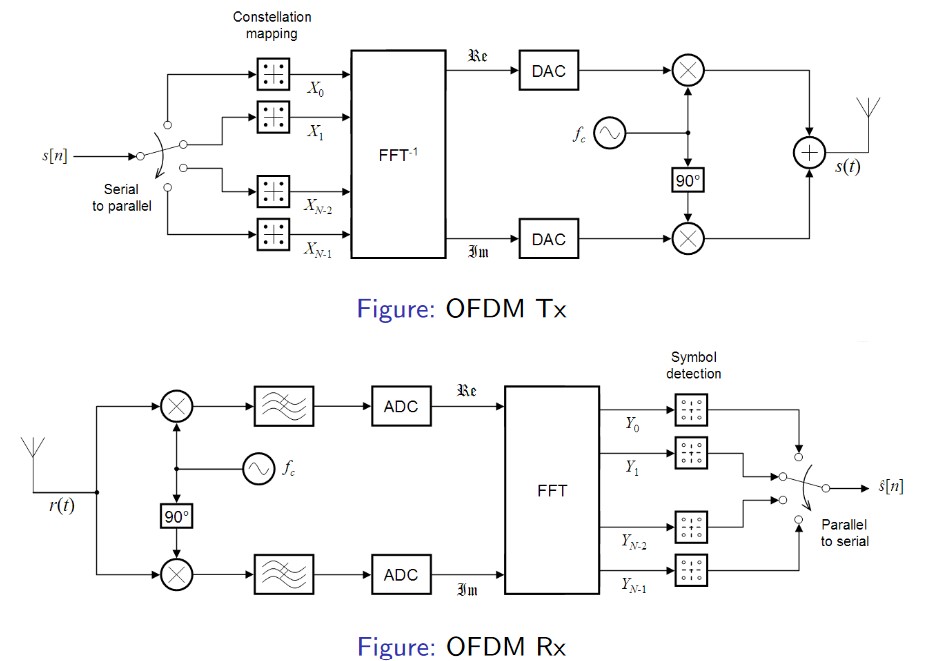
3. 希尔伯特变换
那么上面的这个系统跟希尔伯特变换又有什么关系呢?
首先我们来从时域和频域分别看一下希尔伯特变换: \[ \begin{aligned} h(t) &= \frac{1}{\pi t} \\ H(f) &= -j \operatorname{sgn}(f) \end{aligned} \] 希尔伯特变换实际上是一个使相位滞后pi/2的全通移相网络,比如信号 \(\cos(\omega t)\) 经过希尔伯特滤波器后就变成 \(\sin(\omega t)\)。另外希尔伯特变换还有一个性质就是 \(H^2(f) = -1\),即经过两次变换之后就是原信号的反相。
那么再回到通信系统里边。基于傅里叶变换我们知道,一个复信号可以表示成 \(x(t) = \int X(f)\exp(j2\pi f t) df\),即时域和频域是对应的,可以相互转化,我们记成 \[ x(t) \longleftrightarrow X(f) \] 假设 \(x(t)\) 用其实部和虚部表示 \(x(t) = a(t) + jb(t)\),那么有 \[ \begin{aligned} a(t) &\longleftrightarrow \frac{X(f) + X^{*}(-f)}{2} \\ b(t) &\longleftrightarrow \frac{X(f) - X^{*}(-f)}{2j} \end{aligned} \] 对于一个单边带信号 \(x(t)\),\(X(f)\) 只在正(或负)频率非零,那么 \(X(f)\) 和 \(X^{*}(-f)\) 是没有频谱重叠的,所以我们可以看到 \(b(t)\) 实际上就是 \(a(t)\) 的希尔伯特变换,也即: \[ \begin{aligned} b(t) &= \mathcal{H}(a(t)) \\ a(t) &= -\mathcal{H}(b(t)) \end{aligned} \] 所以只需要信号 \(x(t)\) 的实部 \(a(t)\)(或只需要虚部 \(b(t)\))我们就能恢复出完整的复信号 \(x(t)\)。
联想第 2 节的系统,想要在收发端传输的是单边带复信号 \(x(t)\exp(j2\pi f_c t)\),实际上只发射了它的实部 \(z(t) = \text{Re}\left\{ x(t)\exp(j2\pi f_c t) \right\}\),尽管如此我们在接收端还是可以只根据其实部就恢复出完整的信号,这就可以用希尔伯特变换来解释。
但是需要注意的是,这只适用于单边带信号!双边带信号的实部和虚部并没有这种关系,因此不能仅通过实部或虚部恢复完整复信号!