泛函分析笔记5:Hahn-Banach定理的应用
1. 共轭算子
赋范空间 \(X,Y\),\(T\in B(X,Y)\),对于任意的 \(f\in Y'\),\(X \stackrel{T}{\longrightarrow}Y\stackrel{f}{\longrightarrow}\mathbb{K}\),可以得到 \(f\circ T\in X'\)。因此我们可以定义映射 \[ \begin{aligned} T^{\times}:Y' &\to X' \\ f &\mapsto f\circ T \end{aligned} \] 称其为共轭算子。他有如下性质(容易验证,不再证明):
- \(T^{\times}\in B(Y',X')\)
- \(\Vert T^{\times}\Vert=\Vert T\Vert\)(证明过程用到了 Hahn-Banach定理)
- \((S+T)^{\times}=S^\times + T^\times,\ S,T\in B(X,Y)\)
- \((\lambda T)^\times=\lambda T^\times\)
- \((AB)^\times=B^\times A^\times,\ A\in B(X,Y),B\in B(Y,Z)\)
例子 1:设 \(X=Y=\mathbb{C}^n,T\in B(\mathbb{C}^n,\mathbb{C}^n)\),则 \(\exists!A\) 为 \(n\) 阶方阵使得 \(Tx=Ax\),而 \(T^\times\in B((\mathbb{C}^n)',(\mathbb{C}^n)')\)。实际上 \(f\in(\mathbb{C}^n)'\) 可以表示为 \(f(x)=\sum_i^n \alpha_i x_i=\alpha^T x\),\(T^\times f(x)=\sum_i^n\beta_i x_i=\beta^T x\)。容易验证 \(\beta=A^T\alpha.\)
在这里,我们可以联想到伴随算子,\(T\in B(H_1,H_2)\),其伴随算子 \(T^\star\in B(H_2,H_1)\) 满足 \(\langle Tx,y\rangle=\langle x,T^\star y\rangle.\) 而这里的共轭算子则是 \(T^\times\in B(H_2', H_1').\)
回忆第二章我们讲等距同构概念的时候,提到了 \((\mathbb{K}^n,\Vert\cdot\Vert_2)' = (\mathbb{K}^n,\Vert\cdot\Vert_2)\),也就是说实际上我们可以找到某个映射 \(A:H'\to H\)。如果能找到这样的一个双射,就可以认为 \(T^\star\) 与 \(T^\times\) 是等价的。
一般的空间未必有如此良好的性质,但对于 Hilbert 空间来说,任意 \(f\in H'\) 都可以唯一地表示为 \(f(x)=\langle x,z\rangle, z\in H\),那么我们就可以定义映射 \[ \begin{aligned} A:H' &\to H \\ f &\mapsto z \end{aligned} \] 容易证明 \(A\) 时共轭线性的(并且是双射),即 \(A(\lambda f+\mu g)=\bar{\lambda}Af+\bar{\mu}Ag\)。
此时我们可以得到如下图所示的映射关系,可以看到实际上 \(T^\times = A_1^{-1}T^\star A_2\)
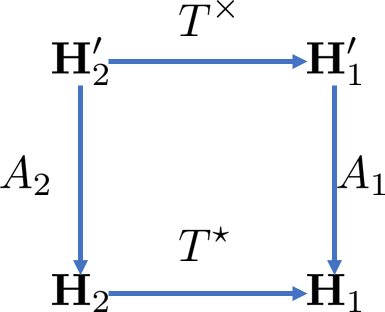
例子 2:考虑 Hilbert 空间 \(H_1,H_2\),\(g\in H_2'\) 可以表示为 \(g(y)=\langle y,y_0\rangle\),因此实际上有 \(A_2g=y_0\in H_2\),令 \(f=T^\times g\in H_1'\),因此可以表示为 \(f(x)=\langle x,x_0\rangle\),这可以表示为 \(A_1f=x_0\in H_1\),因此有 \(A_1T^\times g=x_0\),结合 \(A_1T^\times = T^\star A_2\) 就有 \(x_0=T^\star y_0.\)
2. 自反空间
前面我们研究了 \(X\) 与 \(X'\) 的关系,当 \(X\) 为 Hilbert 空间时二者等距同构。这一小节我们想再研究研究 \(X\) 与 \(X''\) 的关系。为什么要研究他们的关系呢?因为不论原始空间 \(X\) 怎么样,对偶空间 \(X'\) 总是 Banach 空间。友情提示,接下来这部分会比较绕。
2.1 典范映射
如果想要研究 \(X\) 与 \(X''\) 的关系,考虑映射 \(J:X\to X''\),那么就需要考虑 \(J\) 是否是等距同构的,或者是否是单射、满射、双射?如何定义 \(J\) 呢?考虑 \(J(x)\in X''\),记 \(g_x=J(x): X'\to\mathbb{K}\),即 \[ \begin{aligned} J:X&\to X'' \\ x&\mapsto g_x \end{aligned} \] 那么对于任意 \(f\in X'\),定义 \(g_x(f)=f(x)\in\mathbb{K}\),因此 \((J(x))(f)=f(x)\)。其中 \(x\) 为 \(J\) 的自变量,\(J(x)\) 是一个泛函,\(f\) 为 \(J(x)\) 的自变量。
首先来看按照上面的方法给出的 \(J\) 的定义是否满足 \(J:X\to X''.\) 首先来看 \(J(x)=g_x\) 是否为 \(X'\) 上的线性泛函?\(g_x(\lambda f+\mu h)=\lambda f(x)+\mu h(x)=\lambda g_x(f)+\mu g_x(h)\),因此 \(g_x\in (X')^\star\),接下来还需要验证 \(\Vert g_x\Vert\) 是否是有界的。 \[ \Vert g_x\Vert = \sup_{f\in X'}\frac{\Vert g_x(f)\Vert}{\Vert f\Vert} = \sup_{f\in X'}\frac{|f(x)|}{\Vert f\Vert} = \Vert x\Vert \] 因此有 \(J(x)=g_x\in X'',\forall x\in X\),说明我们定义的 \(J\) 确实是 \(X\to X''\) 的映射,我们称之为典范映射。
那么这个映射有什么性质呢?\(J\) 是否为线性映射?\(g_{\lambda x+\mu y}=J(\lambda x+\mu y)\in X''\),对于 \(\forall f\in X'\),都有 \[ g_{\lambda x+\mu y}(f)=f(\lambda x+\mu y)=\lambda f(x)+\mu g(y)=\lambda g_x(f)+\mu g_y(f) \\ \Longrightarrow g_{\lambda x+\mu y} = \lambda g_x+\mu g_y\\ \Longrightarrow J(\lambda x+\mu y) = \lambda J(x) + \mu J(y) \] 这说明 \(J\) 是线性映射,那么 \(\Vert J\Vert\) 是多少?是否是有界线性映射? \[ \Vert J\Vert = \sup_{x\in X} \frac{\Vert J(x)\Vert}{\Vert x\Vert},\quad \Vert J(x)\Vert=\Vert x\Vert \] 因此 \(\Vert J\Vert = 1.\)
由于任意 \(x\in X\) 都可以得到 \(J(x)\in X''\),因此 \(X\) 可以视为 \(X''\) 的“赋范子空间”,也就是说 \(X\) 的势小于 \(X''\)。那么是否有 \(X''\) 的势就等于 \(X\) 的势呢?如果二者势相等,由于 \(J\) 是保范映射,就说明 \(X\) 与 \(X''\) 是等距同构的!但是遗憾的是并不是任意赋范空间 \(X\) 都有这个结论,只有某些条件下,比如 Hilbert 空间有这个性质。
若 \(J\) 为满射,则称 \(X\) 为自反空间(意味着 \(X\) 与 \(X''\) 等距同构),这有如下两种等价表示: \[ \begin{aligned} \iff& \forall F\in X'',\quad \exists! x\in X,\quad F=J(x) \\ \iff& \forall F\in X'',\quad \exists! x\in X,\quad F(f)=f(x),\forall f\in X' \end{aligned} \]
如果 \(X\) 为自反的,由于 \(X''\) 为 Banach 空间,那么 \(X\) 也是 Banach 空间。
命题:Hilbert 空间均为自反的。
证明:这个证明的思路非常巧妙!直接按照上面的定义来证明很难证出来。为此我们首先考虑 \(H'\),我们已经知道他是 Banach 空间了,但它实际上是一个 Hilbert 空间,怎么证明呢?
对 \(\forall f,g\in H'\),我们前面提到 \(f(x)=\langle x,Af\rangle, Af\in H\),因此定义 \[ \langle f,g\rangle_1 = \langle Ag, Af\rangle \] 验证内积的定义可以证明 \(\langle \cdot,\cdot\rangle_1\) 就是 \(H'\) 上的内积,因此 \(H'\) 是 Hilbert 空间。这样的话就太好了,因为 \(\forall F\in H''\),都存在唯一的 \(f_0\in H'\),使得 \(F(f)=\langle f,f_0\rangle_1=\langle Af_0, Af\rangle=f(Af_0)\)!因此 \(H\) 为自反空间。证毕。
例子 1:若 \(1<p<\infty\),\(\ell^p\) 是自反的。
证明:我们首先知道 \((\ell^p)'\) 与 \(\ell^q\) 是等距同构的,而 \((\ell^p)''=(\ell^q)'=\ell^p\),因此 \(\ell^p\) 是自反的(\(1/p+1/q=1\))。
不过这个证明不太严谨,也可以利用自反空间的等价定义(跟上面的表述是等价的)。任意的 \(f\in (\ell^p)'\),可以表示为 \(f(x)=\langle x,y\rangle,x\in\ell^p,y\in\ell^q\),对任意的 \(F\in(\ell^p)''\),现在问题来了,\(F(f)\) 是个什么东西?我们怎么定义 \(F(f)\)?\(f\) 是一个函数,如何将其映射到 \(\mathbb{K}\) 上去呢?这是时候还是要应用等距同构的性质,\((\ell^p)'\) 与 \(\ell^q\) 等距同构,因此我们可以用 \(y\in\ell^q\) 来等价的代替 \(f\in(\ell^p)'\),这样的话 \(F(f)\) 就很容易定义了,\(F(f)\triangleq F_1(y)\in\mathbb{K}\),那么我们就能找到唯一的 \(x_0\in\ell^p\),使得 \(F_1(y)=\langle y,x_0\rangle=\langle x_0,y\rangle=f(x_0)\),这样的话任意 \(F\in (\ell^p)''\),我们都能找到对应的唯一的 \(x_0\in \ell^p\),使得 \(F(f)=f(x_0)\)。证毕。
例子 2:有限维赋范空间自反。
证明:假设 \(\text{dim}X=n<\infty\),那么应用 Hamel 基的性质(参考教材例 2.5.3)\(\text{dim}X^\star=n\)。再应用下面的引理(可参考第2章),可以知道有限维赋范空间的 \(X'=X^\star\) 等距同构,因此 \(\text{dim}X'=n\),因此也有 \(\text{dim}X''=n\),因此 \(J:X\to X''\) 为满射,\(X\) 为自反的。证毕。
引理:\(X,Y\) 为 \(\mathbb{K}\) 上的赋范空间,假设 \(\text{dim}X=n<\infty\),\(T:X\to Y\) 是线性算子,那么 \(T\) 一定是有界的。
2.2 可分性
研究集合的可分性,可以通过验证典范映射 \(J\) 是否为双射,也有另一个思路,就是下面要讲的可分性。
定理(Hahn-Banach) 5:\((X,\Vert\cdot\Vert)\),\(Y\) 为 \(X\) 的线性子空间,\(Y\subsetneq X\),对 \(\forall x_0\in Y^c\),令 \[ \delta = \rho(x_0,Y)=\inf_{y\in Y}\Vert x_0-y\Vert \] 则存在 \(f\in X'\),使得 \(\Vert f\Vert=1, f|_Y=0,f(x_0)=\delta.\)
NOTE:这个定理在说什么事呢?前面在讲内积空间的时候,我们提到了 Hilbert 空间上的有界线性泛函实际上可以表示为 \(f(x)=\langle x,z_0\rangle\),这实际上可以看成是以 \(z_0\) 为法向量的超平面,因此 \(N(f)^{\perp}\) 是一维的,也就是说 \(f\) 在 \(z_0\) 方向上是非零的,在正交于 \(z_0\) 的平面内都是 0。而这个定理当中,寻找这个 \(f\) 要做的就是找到一个合适的法向量,使得 \(z_0\perp Y\),并且添加一个线性系数使得刚好有 \(f(x_0)=\delta\)。不过这个定理更加强大的一个地方在于不要求 \(X\) 是 Hilbert 空间,只要求赋范空间即可。
证明:考虑 \(M=\text{span}(Y\cup \{x_0\})\) 是 \(X\) 的线性子空间,则 \(\forall x\in M\),存在唯一的分解方式 \(x=y+\lambda x_0\),\(y\in Y,\lambda\in\mathbb{K}\),定义 \(f_0(x)=\lambda \delta.\) 容易验证 \(f_0\in M', \Vert f_0\Vert\le1\),也可以验证 \(\Vert f_0\Vert \ge1\)(需要思考一下)。因此存在 \(f\in X'\) 使得 \(\Vert f\Vert=\Vert f_0\Vert\),\(f|_Y=f_0|_Y=0\),并且 \(f(x_0)=f_0(x_0)=\delta.\) 证毕。
推论:\((X,\Vert\cdot\Vert)\),若 \(X'\) 为可分空间,则 \(X\) 为可分空间。
NOTE:这个推论可用于证明某个空间不是自反空间:如果 \(X\) 可分,但是 \(X’\) 不可分,那么 \(X\) 一定不自反。否则的话 \(X''=X\) 是可分的,应该有 \(X'\) 也是可分的,矛盾。
证明: 参考教材,略。
例子 3:\(c_o,\ \ell^1,\ \ell^\infty,\ C[a,b]\) 都不是自反空间。
证明:\(c_0'=\ell^1,(\ell^1)'=\ell^\infty, (\ell^\infty)'=\ell^1\)(参考课本 P68),但是由于 \(c_0,\ell^1\) 是可分的,而 \(\ell^\infty\) 不是可分的,因此 \(\ell^1\) 不自反。
\(C[a,b]'\) 是不可分的,\(C[a,b]\) 是可分的, 细节参考课本,懒得写了......后面心情好了再补吧......
3. Riemann-Stieltjes积分
称函数 \(\omega:[a,b]\to\mathbb{K}\) 为有界变差函数,若存在常数 \(C\ge0\),使得任取 \([a,b]\) 的分划 \[ a=t_0<t_1<\cdots<t_n=b \] 都有 \(\sum_{i=1}^n |\omega(t_i)-\omega(t_{i-1})|\le C\)。记所有 \([a,b]\) 上的有界变差函数构成的集合为 \(BV[a,b]\)。并定义 \([a,s],a\le s\le b\) 上的全变差为 \[ \text{Var}_{[a,s]}(\omega)=\sup\sum_{i=1}^n |\omega(t_i)-\omega(t_{i-1})| \] 其中上确界是对所有 \([a,s]\) 上的分划来取。
命题:若 \(\omega:[a,b]\to\mathbb{R}\) 单调,则 \(\omega\in BV[a,b]\),并且此时有 \(\text{Var}_{[a,b]}(\omega)=|\omega(b)-\omega(a)|.\)
命题:若 \(\omega:[a,b]\to \mathbb{R}\) 为有界变差的,则存在 \(\omega_1,\omega_2\) 单调递增,使得 \(\omega=\omega_1-\omega_2.\)
证明:取 \(\omega_1(t)=\text{Var}_{[a,t]}(\omega)\),那么易证 \(\omega_1\) 是单调递增的。取 \(\omega_2=\omega-\omega_1\) 也是递增的,这是因为 \(\forall t<s\),\(t,x\in[a,b]\) 都有 \[ \begin{aligned} \omega_2(s)-\omega_2(t) &=\text{Var}_{[a,s]}(\omega)-\text{Var}_{[a,t]}(\omega)-\omega(s)+\omega(t) \\ &=\text{Var}_{[t,s]}(\omega)-(\omega(s)-\omega(t)) \ge 0 \end{aligned} \] 其中第二个等号用到了下面的引理。
引理:\(\text{Var}_{[a,s]}(\omega)=\text{Var}_{[a,t]}(\omega)+\text{Var}_{[t,s]}(\omega).\)
证明:略。
在 \(BV[a,b]\) 上定义范数 \(\Vert \omega\Vert_{bv}=\text{Var}_{[a,b]}(\omega)+|\omega(a)|\),则可以证明 \(\Vert\cdot\Vert_{bv}\) 为 \(BV[a,b]\) 上的范数,并且 \(BV[a,b]\) 为 Banach 空间。
对 \(\forall \omega\in BV[a,b], x\in C[a,b]\),若 \(\mathcal{P}\) 为 \([a,b]\) 的分划 \(a=t_0<t_1<\cdots<t_n=b\),令 \[ S(x,\omega,\mathcal{P})=\sum_{i=1}^n x(t_{i-1})(\omega(t_i)-\omega(t_{i-1})) \] 是 \(x\) 关于有界变差函数 \(\omega\) 和分划 \(\mathcal{P}\) 的 Darboux 和。记 \(\eta(\mathcal{P})=\max_i (t_i-t_{i-1}) \to 0\),若存在唯一的 \(A\in\mathbb{K}\) 使得 \(S(x,\omega,\mathcal{P})\to A\),则称 \(A\) 为 \(x\) 关于 \(\omega\) 的 Riemann-Stieltjes 积分,记为 \[ A = \int_a^b x(t)d\omega(t). \] 定义线性泛函 \(\phi_{\omega}:C[a,b]\to\mathbb{K}\) 为 \[ \phi_\omega(x)=\int_a^b x(t)d\omega(t) \] 则 \(\phi_\omega\in C[a,b]'\),并且有 \(\Vert \phi_\omega\Vert\le \text{Var}_{[a,b]}(\omega)\)。
定理:\(\forall \phi\in C[a,b]'\),\(\exists! \omega\in BV[a,b]\),满足 \(\omega(a)=0\),\(\forall x\in C[a,b]\),\(\phi(x)=\int_a^b x(t)d\omega(t)\),此时有 \(\Vert \phi\Vert=\Vert\omega\Vert_{bv}.\)
证明:略。