凸优化笔记15：梯度方法 Gradient Method

前面的章节基本上讲完了凸优化相关的理论部分，在对偶原理以及 KKT 条件那里我们已经体会到了理论之美！接下来我们就要进入求解算法的部分，这也是需要浓墨重彩的一部分，毕竟我们学习凸优化就是为了解决实际当中的优化问题。我们今天首先要接触的就是大名鼎鼎的梯度方法。现在人工智能和人工神经网络很火，经常可以听到反向传播，这实际上就是梯度下降方法的应用，他的思想其实很简单，就是沿着函数梯度的反方向走就会使函数值不断减小。 \[ x_{k+1}=x_{k}-t_k \nabla f(x_k),\quad k=0,1,... \] 上面的式子看起来简单，但是真正应用时你会发现有各种问题：

下降方向怎么选？\(\nabla f(x_k)\) 吗？选择其他方向会不会好一点呢？
如果 \(f(x)\) (在某些点)不可导又怎么办呢？
步长 \(t_k\) 怎么选呢？固定值？变化值？选多大比较好？
收敛速度怎么样呢？我怎么才能知道是否达到精度要求呢？
...

1. 凸函数

前面讲凸函数的时候我们提到了很多等价定义：Jensen's 不等式、“降维打击”、一阶条件、二阶条件。这里我们主要关注其中两个：

Jensen's 不等式：\(f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y)\)
一阶条件等价于梯度单调性：\((\nabla f(x)-\nabla f(y))^{T}(x-y) \geq 0 \quad \text { for all } x, y \in \operatorname{dom} f\)

也就是说凸函数的梯度 \(\nabla f: R^n\to R^n\) 是一个单调映射。

2. Lipschitz continuity

函数 \(f\) 的梯度满足利普希茨连续(Lipschitz continuous)的定义为 \[ \|\nabla f(x)-\nabla f(y)\|_{*} \leq L\|x-y\| \quad \text { for all } x, y \in \operatorname{dom} f \] 也被称为 L-smooth。有了这个条件，我们可以推出很多个等价性质，这里省略了证明过程

也就是说下面的式子都是等价的 \[ \|\nabla f(x)-\nabla f(y)\|_{*} \leq L\|x-y\| \quad \text { for all } x, y \in \operatorname{dom} f \]

\[ (\nabla f(x)-\nabla f(y))^{T}(x-y) \leq L\|x-y\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f \]

\[ f(y) \leq f(x)+\nabla f(x)^{T}(y-x)+\frac{L}{2}\|y-x\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f \]

\[ (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq \frac{1}{L}\|\nabla f(x)-\nabla f(y)\|_{*}^{2} \quad \text { for all } x, y \]

\[ g(x)=\frac{L}{2}\Vert x\Vert_2^2-f(x) \ \text{ is convex} \]

Remarks 1：

上面的第 3 个式子 \[ f(y) \leq f(x)+\nabla f(x)^{T}(y-x)+\frac{L}{2}\Vert y-x\Vert^{2} \quad \text { for all } x, y \in \operatorname{dom} f \] 实际上定义了一个二次曲线，这个曲线是原始函数的 Quadratic upper bound

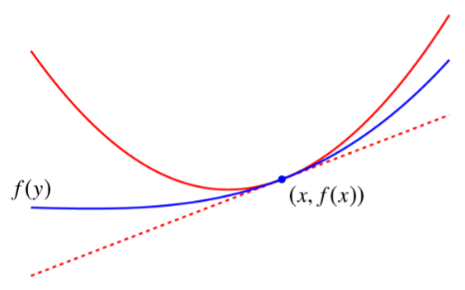
并且由这个式子可以推导出 \[ \frac{1}{2 L}\Vert\nabla f(z)\Vert_{*}^{2} \leq f(z)-f\left(x^{\star}\right) \leq \frac{L}{2}\left\Vert z-x^{\star}\right\Vert^{2} \quad \text { for all } z \] 这个式子中的上界 \(\frac{L}{2}\left\|z-x^{\star}\right\|^{2}\) 带有 \(x^\star\) 是未知的，而下界只与当前值 \(z\) 有关，因此在优化过程中我们可以判断当前的 \(f(z)\) 与最优值的距离至少为 \(\frac{1}{2 L}\|\nabla f(z)\|_{*}^{2}\)，如果这个值大于0，那么我们一定还没得到最优解。

Remarks 2：

上面的最后一个式子 \[ (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq \frac{1}{L}\|\nabla f(x)-\nabla f(y)\|_{*}^{2} \quad \text { for all } x, y \] 被称为 \(\nabla f\) 的 co-coercivity 性质。（这其实有点像 \(\nabla f\) 的反函数的 L-smooth 性质，所以它跟 \(\nabla f\) 的 L-smooth 性质是等价的）

3. 强凸函数

满足如下性质的函数被称为 m-强凸(m-strongly convex)的 \[ f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y)-\frac{m}{2} \theta(1-\theta)\|x-y\|^{2} \quad \text { for all } x, y\in\text{dom}f,\theta\in[0,1] \] m-强凸跟前面的 L-smooth 实际上非常像，只不过一个定义了上界，另一个定义了下界。

类似上面的 L-smooth 性质，我们课可以得到下面几个式子是等价的 \[ f \text{ is m-strongly convex} \]

\[ (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq m\|x-y\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f \]

\[ f(y) \geq f(x)+\nabla f(x)^{T}(y-x)+\frac{m}{2}\|y-x\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f \]

\[ g(x) = f(x)-\frac{m}{2}\Vert x\Vert^2 \ \text{ is convex} \]

注意上面第3个式子不等号右遍实际上又定义了一个二次曲线，这个二次曲线是原函数的下界。与前面的二次上界类比可以得到

Quadratic lower bound	Quadratic upper bound

\(f(y) \geq f(x)+\nabla f(x)^{T}(y-x)+\frac{m}{2}\Vert y-x\Vert^{2}\)	\(f(y) \leq f(x)+\nabla f(x)^{T}(y-x)+\frac{L}{2}\Vert y-x\Vert^{2}\)
\(\Longrightarrow \frac{m}{2}\left\Vert z-x^{\star}\right\Vert^{2} \leq f(z)-f\left(x^{\star}\right) \leq \frac{1}{2 m}\Vert\nabla f(z)\Vert_{*}^{2}\)	\(\Longrightarrow \frac{1}{2 L}\Vert\nabla f(z)\Vert_{*}^{2} \leq f(z)-f\left(x^{\star}\right) \leq \frac{L}{2}\left\Vert z-x^{\star}\right\Vert^{2}\)

例子：如果函数 \(f\) 既是 m-强凸的，又是(关于2范数) L-smooth 的，那么

函数 \(h(x)=f(x)-\frac{m}{2}\Vert x\Vert^2\) 是 (L-m)-smooth 的
函数 \(h\) 的 co-coercivity 可以写为

\[ (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq \frac{m L}{m+L}\|x-y\|_{2}^{2}+\frac{1}{m+L}\|\nabla f(x)-\nabla f(y)\|_{2}^{2} \quad \text { for all } x, y \in \operatorname{dom} f \]

4. 梯度方法收敛性分析

下面给出一些常见梯度下降方法的分析。先回顾一下梯度方法的一般表达式 \[ x_{k+1}=x_{k}-t_k \nabla f(x_k) \] 首先有一些假设

\(f\) convex 且可导，\(\text{dom}f=R^n\)
\(\nabla f\) 关于2范数 L-Lipschitz continuous
最优解有限且可取

4.1 固定步长

固定步长为 \(t\)，则 \(x^+=x-t\nabla f(x)\)，根据 L-smooth 性质有 \[ f(x-t \nabla f(x)) \leq f(x)-t\left(1-\frac{L t}{2}\right)\|\nabla f(x)\|_{2}^{2} \] 如果 \(0 < t \leq 1/L\)，则有 \[ f\left(x^{+}\right) \leq f(x)-\frac{t}{2}\|\nabla f(x)\|_{2}^{2} \] 这表明(只要步长 \(t\) 比较小)函数值总是在不断减小的。从上面的式子结合凸函数性质我们还可以得到 \[ \begin{aligned} f\left(x^{+}\right)-f^{\star} & \leq \nabla f(x)^{T}\left(x-x^{\star}\right)-\frac{t}{2}\|\nabla f(x)\|_{2}^{2} \\ &=\frac{1}{2 t}\left(\left\|x-x^{\star}\right\|_{2}^{2}-\left\|x-x^{\star}-t \nabla f(x)\right\|_{2}^{2}\right) \\ &=\frac{1}{2 t}\left(\left\|x-x^{\star}\right\|_{2}^{2}-\left\|x^{+}-x^{\star}\right\|_{2}^{2}\right) \end{aligned} \] 从这个式子可以得到我们到最优点 \(x^\star\) 的距离在不断减小。那么可以得到下面的式子 \[ \begin{aligned} \sum_{i=1}^{k}\left(f\left(x_{i}\right)-f^{\star}\right) & \leq \frac{1}{2 t} \sum_{i=1}^{k}\left(\left\|x_{i-1}-x^{\star}\right\|_{2}^{2}-\left\|x_{i}-x^{\star}\right\|_{2}^{2}\right) \\ &=\frac{1}{2 t}\left(\left\|x_{0}-x^{\star}\right\|_{2}^{2}-\left\|x_{k}-x^{\star}\right\|_{2}^{2}\right) \\ & \leq \frac{1}{2 t}\left\|x_{0}-x^{\star}\right\|_{2}^{2} \end{aligned} \\ \Longrightarrow f(x_k)-f^\star\leq\frac{1}{k}\sum_{i=1}^{k}\left(f\left(x_{i}\right)-f^{\star}\right) \leq \frac{1}{2 kt}\left\|x_{0}-x^{\star}\right\|_{2}^{2} \] 因此普通的固定步长的梯度下降有以下收敛性质

\(f(x_{k+1}) < f(x_k)\)
\(\Vert x_{k+1}-x^\star\Vert < \Vert x_{k}-x^\star\Vert\)
\(f(x_k)-f^\star\leq \frac{1}{2 kt}\left\|x_{0}-x^{\star}\right\|_{2}^{2}\)，要想满足精度 \(f(x_k)-f^\star \leq \epsilon\) 需要的迭代次数为 \(O(1/\epsilon)\)

4.2 线搜索

线搜索就是每步都要计算合适的步长，计算方法为不断地迭代 \(t_k:=\beta t_k,0<\beta<1\) 直到 \(t_k\) 满足下面的条件 \[ f\left(x_{k}-t_{k} \nabla f\left(x_{k}\right)\right)<f\left(x_{k}\right)-\alpha t_{k}\left\|\nabla f\left(x_{k}\right)\right\|_{2}^{2} \] 形象理解就是下面这幅图，一开始我们的 \(t_k\) 可能很大，表示梯度下降的步长过大，不能使函数值减小，那我们就减小步长 \(t_k=\beta t_k\)，直到进入绿线与蓝线交点左侧这部分，我们就可以保证一定有 \(f(x_{k+1})<f(x_k)\)，这时就是我们要取的 \(t_k\)，这也是线搜索的含义，线搜索实际上就是在搜索合适的步长 \(t_k\)。

主要到上面的式子中有一个参数 \(\alpha\) 会影响我们的搜索结果，比如上图中 \(\alpha\) 越大，则绿线的斜率越大，那么最终搜索到的 \(t_k\) 应该就越小，表示我们每一步的步长都会更小。实际中往往取 \(\alpha=1/2\)，此时理想的搜索结果实际上就是 quadratic upper bound 的最小值点。也就是说我们用二次上界曲线来近似待优化的函数，而二次上界的最小值点对应的步长就是 \(t=1/L\)，但由于我们是线搜索，实际得到的 \(t_k\) 一般会比这个值略小一点。

另一方面为了保证线搜索在有限步能够终止，还需要满足 \(t_k\ge t_\min =\min\{\hat{t},\beta/L\}\)，其中 \(\hat{t}\) 是预先指定的一个参数。

那么线搜索的收敛性怎么样呢？首先根据线搜索的定义一定有 \[ \begin{aligned} f\left(x_{i+1}\right) & \leq f\left(x_{i}\right)-\frac{t_{i}}{2}\left\|\nabla f\left(x_{i}\right)\right\|_{2}^{2} \\ & \leq f^{\star}+\nabla f\left(x_{i}\right)^{T}\left(x_{i}-x^{\star}\right)-\frac{t_{i}}{2}\left\|\nabla f\left(x_{i}\right)\right\|_{2}^{2} \\ &=f^{\star}+\frac{1}{2 t_{i}}\left(\left\|x_{i}-x^{\star}\right\|_{2}^{2}-\left\|x_{i+1}-x^{\star}\right\|_{2}^{2}\right) \end{aligned} \] 这表明 \(f(x_{i+1})<f(x_i),\left\|x_{i}-x^{\star}\right\|_{2}>\left\|x_{i+1}-x^{\star}\right\|_{2}\)，类似前面固定步长的分析，可以得到 \[ f(x_k)-f^\star\leq\frac{1}{k}\sum_{i=1}^{k}\left(f\left(x_{i}\right)-f^{\star}\right) \leq \frac{1}{2 kt_\min}\left\|x_{0}-x^{\star}\right\|_{2}^{2} \] 因此对于线搜索的方法，我们可以得到如下的收敛性质

\(f(x_{i+1})<f(x_i)\)
\(\left\|x_{i}-x^{\star}\right\|_{2}>\left\|x_{i+1}-x^{\star}\right\|_{2}\)
\(f(x_k)-f^\star\leq \frac{1}{2 kt_\min}\left\|x_{0}-x^{\star}\right\|_{2}^{2}\)

所以线搜索实际上并不能提高收敛速度的阶，他与固定步长的方法都是 \(O(1/k)\) 的，为 sublinear 收敛。

4.3 一阶方法的收敛极限

不管是固定步长还是线搜索，前面的方法都是一阶方法，即 \[ x_{k+1}\in x_{0}+\operatorname{span}\left\{\nabla f\left(x_{0}\right), \nabla f\left(x_{1}\right), \ldots, \nabla f\left(x_{k}\right)\right\} \] 而理论上也证明一阶方法的收敛速度存在极限。

定理(Nesterov)： for every integer \(k ≤ (n−1)/2\) and every \(x_0\), there exist functions in the problem class such that for any ﬁrst-order method \[ f\left(x_{k}\right)-f^{\star} \geq \frac{3}{32} \frac{L\left\|x_{0}-x^{\star}\right\|_{2}^{2}}{(k+1)^{2}} \] 也就是说收敛速度最多也就是 \(O(1/k^2)\)。

4.4 强凸函数的梯度方法

对于强凸函数，即使采用固定步长的梯度方法，也可以得到线性收敛速度！这就是强凸性带来的好处。

考虑 \(0<t<2/(m+L)\)，我们有 \[ \begin{aligned} \left\|x^{+}-x^{\star}\right\|_{2}^{2} &=\left\|x-t \nabla f(x)-x^{\star}\right\|_{2}^{2} \\ &=\left\|x-x^{\star}\right\|_{2}^{2}-2 t \nabla f(x)^{T}\left(x-x^{\star}\right)+t^{2}\|\nabla f(x)\|_{2}^{2} \\ & \leq\left(1-t \frac{2 m L}{m+L}\right)\left\|x-x^{\star}\right\|_{2}^{2}+t\left(t-\frac{2}{m+L}\right)\|\nabla f(x)\|_{2}^{2} \\ & \leq\left(1-t \frac{2 m L}{m+L}\right)\left\|x-x^{\star}\right\|_{2}^{2} \end{aligned} \] 也就是说可以得到 \[ \left\|x_{k}-x^{\star}\right\|_{2}^{2} \leq c^{k}\left\|x_{0}-x^{\star}\right\|_{2}^{2}, \quad c=1-t \frac{2 m L}{m+L} \\ f\left(x_{k}\right)-f^{\star} \leq \frac{L}{2}\left\|x_{k}-x^{\star}\right\|_{2}^{2} \leq \frac{c^{k} L}{2}\left\|x_{0}-x^{\star}\right\|_{2}^{2} \] 注意到前面是反比例下降，这里变成了指数下降。如果要打到精度 \(f(x_k)-f^\star \leq \epsilon\) 需要的迭代次数为 \(O(\log(1/\epsilon))\)

5. BB 方法

Barzilai-Borwein (BB) method 也是梯度下降方法的一种，他主要是通过近似牛顿方法来实现更快的收敛速度，同时避免计算二阶导数带来的计算复杂度。

如果我们记 \(\boldsymbol{g}^{(k)}=\nabla f\left(\boldsymbol{x}^{(k)}\right) \text { and } \boldsymbol{F}^{(k)}=\nabla^{2} f\left(\boldsymbol{x}^{(k)}\right)\)，那么一阶方法就是 \(\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-\alpha_{k} \boldsymbol{g}^{(k)}\)，其中步长 \(\alpha_k\) 可以是固定的，也可以是线搜索获得的，一阶方法简单但是收敛速度慢。牛顿方法就是 \(\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-\left(\boldsymbol{F}^{(k)}\right)^{-1} \boldsymbol{g}^{(k)}\)，其收敛速度更快，但是海森矩阵计算代价较大。而 BB方法就是用 \(\alpha_{k} \boldsymbol{g}^{(k)}\) 来近似 \(\left(\boldsymbol{F}^{(k)}\right)^{-1} \boldsymbol{g}^{(k)}\)。

怎么近似呢？假如定义 \(s^{(k-1)}:=x^{(k)}-x^{(k-1)} \text { and } y^{(k-1)}:=g^{(k)}-g^{(k-1)}\)，那么海森矩阵实际上就是 \[ \boldsymbol{F}^{(k)}s^{(k-1)}=y^{(k-1)} \] 现在的想法就是用 \((\alpha_k I)^{-1}\) 来近似 \(\boldsymbol{F}^{(k)}\)，那么应该有 \[ (\alpha_k I)^{-1}s^{(k-1)}=y^{(k-1)} \] 这个问题用最小二乘就可以解决了，下面两种选择都可以 \[ \alpha_{k}^{-1}=\underset{\beta}{\arg \min } \frac{1}{2}\left\|s^{(k-1)} \beta-\boldsymbol{y}^{(k-1)}\right\|^{2} \Longrightarrow \alpha_{k}^{1}=\frac{\left(s^{(k-1)}\right)^{T} s^{(k-1)}}{\left(s^{(k-1)}\right)^{T} \boldsymbol{y}^{(k-1)}} \\\alpha_{k}=\underset{\alpha}{\arg \min } \frac{1}{2}\left\|s^{(k-1)}-\boldsymbol{y}^{(k-1)} \alpha\right\|^{2} \Longrightarrow \alpha_{k}^{2}=\frac{\left(\boldsymbol{s}^{(k-1)}\right)^{T} \boldsymbol{y}^{(k-1)}}{\left(\boldsymbol{y}^{(k-1)}\right)^{T} \boldsymbol{y}^{(k-1)}} \] 这两个解有一个微妙的不同点在于 \(\alpha_k^1\) 的分母 \(\left(s^{(k-1)}\right)^{T} \boldsymbol{y}^{(k-1)}\) 有可能等于 0，这会给计算带来麻烦，而 \(\alpha_k^2\) 则不会。

BB方法主要有以下几个特点：