凸优化笔记13:互补性条件
前面我们讲了凸优化问题、对偶原理、拉格朗日函数、KKT 条件,还从几何角度解释了强对偶性,那么这一节将从代数角度解释强对偶性,并给出 KKT 条件中的互补性条件的新的表达形式。
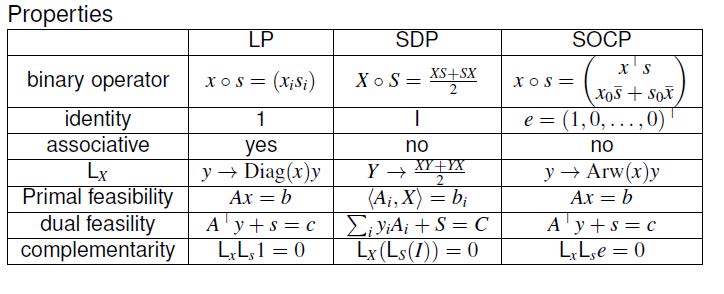
1. LP / SOCP / SDP
在此之前我们先回顾一下比较重要的三类凸优化问题:LP、SOCP、SDP,为什么这么说呢?因为本质上这三类问题非常相似。我们先来回顾一下三类问题 \[ \begin{aligned}LP:\quad \text{minimize} \quad& c^{T} x \\\text{subject to} \quad& A x=b \\& x \succeq 0 \qquad(\bigstar)\\SOCP:\quad \text {minimize} \quad& c^{T} x \\\text {subject to} \quad& Ax=b \\& \left\|\bar{x}\right\|_{2} \leq x_0 \iff x=(x_0,\bar{x})\succeq_Q 0 \qquad(\bigstar)\\SDP:\quad \text{minimize} \quad& \left<C,X\right>\triangleq tr(CX) \quad X\in S^n \\\text{subject to} \quad& A(X)=b \\& X \succeq 0 \qquad(\bigstar)\\\end{aligned} \] 注:上面 SDP 中定义了矩阵内积 \(\left<C,X\right>\triangleq tr(CX)\),这跟向量内积非常类似,而且可以交换 \(\left<C,X\right>=\left<X,C\right>\);还定义了算子 \(A(X)=\left(\left<A_1,X\right>,\cdots,\left<A_n,X\right>\right)\)。
上面三种凸优化问题中,不等式约束都用星号标记出来了,可以看出,他们的形式非常相似,其实都是在不同维度的正常锥里面。不过 LP 的可行域为多面体,最优解往往位于极值点,因此较为简单;但是 SOCP 的可行域则是一个多面体与一个锥的交集,同样的 SDP 和 SOCP 的可行域都是 Nonpolyhedral 的,这就使他们比 LP 要更难求解。
2. 强对偶性的代数解释
考虑 LP 问题及其对偶问题 \[ \begin{aligned} (P):\quad \text{minimize} \quad& c^{T} x \\ \text{subject to} \quad& A x=b \\ & x \succeq 0 \\ (D):\quad \text {maximize} \quad& b^Ty\\ \text {subject to} \quad& A^Ty+s=c \\ & s\succeq0 \end{aligned} \] 那么原问题与对偶问题的 duality gap 就是 \[ c^Tx - b^Ty = x^Ts \] 我们很容易验证 \(x^Ts\ge0\),也就是弱对偶性。如果满足强对偶性(Strong duality)的话,应该有 \[ x^Ts=0 \iff x_is_i=0,i=1,...,n \] 那么我们再来回顾一下 KKT 条件的 4 个部分:
- Primal feasibility:\(Ax=b,x\ge0\)
- Dual feasibility:\(A^Ty+s=c,s\ge0\)
- Complementarity:\(x_is_i=0,i=1,...,n\)
- 梯度条件包含在对偶可行性里面了
因此实际上利用上面 3 个约束就可以求解最优解了。对于上面的互补性条件 \(x_is_i=0\) 我们可以定义一个算子 \[ x\circ s := (x_1s_1,...,x_ns_n)^T = \text{diag}(x)s :=L_xs=L_xL_s\mathbf{1} \] 它满足 \(x\circ \mathbf{1}=x\)。这里其实只是定义了一个新的符号,并没有引入新的东西,之所以这么做是为了与后面的 SOCP、SDP 统一起来用类似的符号表示,便于计算机进行优化计算。
现在我们再来看看 SOCP 问题 \[ \begin{aligned} (P):\quad \text {minimize} \quad& c^{T} x \\ \text {subject to} \quad& Ax=b \\ & x\succeq_Q 0 \\ (D):\quad \text {maximize} \quad& b^{T} y \\ \text {subject to} \quad& A^Ty+s=c \\ & s\succeq_Q 0 \end{aligned} \]
Remarks:注意二阶锥(Second order cone)的对偶锥还是其自身。
对偶锥是其自身怎么直观理解呢?大家想象三维中的这样一个锥,我们任取一个过锥的顶点\((0,0,0)\)的竖直平面,切出来的是应该一个直角吧。那么假如说我们考虑任意的锥呢?切出来的这个角如果不是直角,假如是钝角,那么他的对偶锥一定不是其自身,要比自身“小”,锐角也类似。这里提到这个直观理解在后面会用到。
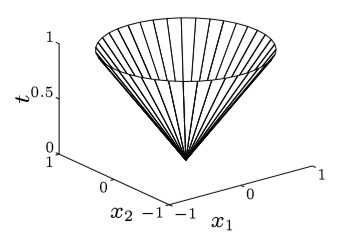
同样的我们可以得到 dualligity gap 为 \[ x^Ts=c^Tx-b^Ty\ge0 \] 如果想得到强对偶性则需要 \[ \begin{aligned}& x^Ts=0,x\succeq_Q 0,s\succeq_Q 0 \\\iff& x_0s_i+x_is_0=0,i=1,...,n \\\iff& x_0\bar{s}+s_0\bar{x}=0\end{aligned} \] 上面这个证明可以利用 Cauchy-Schwarz 不等式 \(x^Ts=x_0s_0+\sum_ix_is_i\ge0\),取等条件即为上式。这从几何角度理解就如下图,其中 \(x,s\) 为正交的,而且他们向后 \(R^n\) 维子空间的投影 \(\bar{x},\bar{s}\) 是反向平行的。

Remarks:\(x,s\) 均为锥 \(Q\) 当中的向量,二者内积为 0,则表明他们相互正交。假如我们固定了 \(x\),\(x\) 作为法向量定义了一个超平面 \(A\),超平面内的任意一个向量都应垂直于 \(x\),所里直观理解的话 \(x\) 应该有无穷多个单位正交向量。但是根据上面的结果,\(s=(s_0,s_0\bar{x}/x_0)\) 只有一个方向,这说明锥 \(Q\) 内部只有一个方向上的向量与 \(x\) 正交!也就是说超平面 \(A\) 与锥 \(Q\) 的交集是一条线,实际上就是说 \(A\) 与 \(Q\) 相切!
再回想一下我们前面提到这个锥 \(Q\) 的顶角应该是一个直角,假如 \(x\) 位于 \(Q\) 的内部(不在边界上),那么 \(A\cap Q=\{(0,0,0)\}\),只有一个点,\(s\) 也就不存在。所以如果想要 \(x^Ts=0\) 有非零解,就一定要求 \(x\) 在 \(Q\) 的边界上,这个时候实际上就有 \(x_0=\Vert\bar{x}\Vert,s_0=\Vert\bar{s}\Vert\) 。这一点很容易从我们上面的式子 \(x_0s_i+x_is_0=0\) 得到验证。
同样得回顾一下 KKT 条件
- \(Ax=b,x\succeq_Q0\)
- \(A^Ty+s=c,s\succeq_Q0\)
- \(x^Ts=0,\quad x_0s_i+x_is_0=0\)
这里再定义一个算子 \[ x\circ s = \left(\begin{array}{c}x_{0} \\x_{1} \\\vdots \\x_{n}\end{array}\right) \circ\left(\begin{array}{c}s_{0} \\s_{1} \\\vdots \\s_{n}\end{array}\right)=\left(\begin{array}{c}x^{\top} s \\x_{0} s_{1}+s_{0} x_{1} \\\vdots \\x_{0} s_{n}+s_{0} x_{n}\end{array}\right) \\ \] 为了简化表示可以写成下面的形式,这样跟 LP 就统一了。 \[ L_{x}=\operatorname{Arw}(x)=\left(\begin{array}{ll}x_{0} & \bar{x}^{\top} \\\bar{x} & x_{0} I\end{array}\right) \notag\\x \circ s=\operatorname{Arw}(x) s=\operatorname{Arw}(x) \operatorname{Arw}(s) e \] 算子满足性质
- \(x\circ s = s\circ x\)
- \(x\circ(x\circ x)=(x\circ x)\circ x\)
- \(x \circ\left(x^{2} \circ y\right)=x^{2} \circ(x \circ y)\)
- \(e=(1,0,...,0)^T,x\circ e=x\)
但是注意不满足结合律 \(x \circ(y \circ z) \neq(x \circ y) \circ z\) 。
最后我们再来看看 SDP 问题及其对偶问题 \[ \begin{aligned}(P):\quad \text{minimize} \quad& \left<C,X\right> \\\text{subject to} \quad& \left<A_i,X\right>=b_i,i=1,...,m \\& X \succeq 0\\(D):\quad \text{minimize} \quad& b^Ty \\\text{subject to} \quad& \sum_i y_iA_i+S=C \\& S\succeq 0\end{aligned} \] 同样的 duality gap 为 \[ \begin{aligned}\left<X,S\right> &= \left<C,X\right> - b^Ty \\&= \left<X,S^{1/2}S^{1/2}\right> = \left<S^{1/2}X,S^{1/2}\right> \ge0\end{aligned} \] 强对偶性则要求 \[ X\succeq0,S\succeq0,\left<X,S\right>=0 \iff XS=0 \iff \frac{XS+SX}{2}=0 \] 证明:\(\left<X,S\right>=\left<S^{1/2}X^{1/2},X^{1/2}S^{1/2}\right>=0 \iff X^{1/2}S^{1/2}=0\)
为了简化表达,我们再定义一个算子 \(X\circ S=\frac{XS+SX}{2}\),它满足以下性质
- \(X\circ S = S\circ X\)
- \(X\circ(X\circ X)=(X\circ X)\circ X\)
- \(X \circ\left(X^{2} \circ Y\right)=X^{2} \circ(X \circ Y)\)
- \(X\circ I = X\)
注意不满足结合律 \(X \circ(Y \circ Z) \neq(X \circ Y) \circ Z\)
再来复习一下 KKT 条件
- \(\left<A_i,X\right>=b_i\)
- \(\sum_i y_iA_i+S=C\)
- \(X\circ S=0\)
最后我们总结一下