凸优化笔记 7:拟凸函数 Quasiconvex Function
1. 拟凸函数定义
拟凸函数(quasiconvex function)的定义为:若 \(\text{dom}f\) 为凸集,且对任意的 \(\alpha\),其下水平集 \[ S_\alpha = \{x\in\text{dom}f | f(x)\le\alpha\} \] 都是凸集,则 \(f\) 为拟凸函数。
类似的有拟凹函数(quasiconcave)的定义。如果一个函数既是拟凸的,又是拟凹的,那么它是拟线性(quasilinear)的。
Reamrks:对于拟线性函数,要求其上水平集和下水平集同时是凸集,因此简单理解,其在某种意义上具有“单调性”。比如 \(e^x,\log x\) 等。
| 拟凸函数 | 各种函数的关系 |
|---|---|
 |
 |
一些常见的拟凸/拟凹/拟线性函数比如
拟凸函数
- \(f(x)=\sqrt{|x|}\)
- \(f(x)=\frac{\Vert x-a\Vert_2}{\Vert x-b\Vert_2},\text{dom}f=\{x|\Vert x-a\Vert_2 \le \Vert x-b\Vert_2\}\)
拟凹函数
- \(f(x)=x_1x_2\) on \(R^2\)
拟线性函数
- \(\text{ceil}(x)=\inf\{z\in Z|z\ge x\}\)
- \(\log x\) on \(R_{++}\)
- \(f(x)=\frac{a^Tx+b}{c^Tx+d},\text{dom}f=\{c^Tx+d >0\}\) (注意 \(f\) 本身不是凸函数,但是是一个保凸变换)
2. 拟凸函数的判定/等价定义
对于普通凸函数,有一些等价定义,比如
- Jensen 不等式 / 凸函数原生定义:\(f(\theta x+(1-\theta)y)\le \theta f(x)+(1-\theta)f(y)\)
- “降维打击”:\(g(t)=f(x+tv)\) convex \(\iff f(x)\) convex
- 一阶条件:\(f(x)\) convex \(\iff f(y)\ge \nabla f^T(x)(y-x)\)
- 二阶条件:\(f(x)\) convex \(\iff \nabla f^2(x)\succeq 0\)
- epigraph:\(f(x)\) convex \(\iff \text{epi}f\) convex
2.1 Jensen 不等式
等价定义 1:函数 \(f\) 为拟凸的等价于:定义域为凸集,且 \[ 0\le\theta\le1 \Longrightarrow f(\theta x+(1-\theta)y)\le\max\{f(x),f(y)\} \] 证明可以直接用定义。
2.1 “降维打击”
等价定义 2:\(g(t)=f(x+tv)\) quasiconvex \(\iff f(x)\) quasiconvex
证明可以直接用定义。
Reamrks:这种“降维打击”的定义方式实际上就是要求 \(f\) 沿着任意一个方向都是(拟)凸的,对于一些高维空间中难以判定凸性,而其一维形式又比较简单的函数来说较适用,比如下面的二阶条件的证明。
2.2 一阶条件
等价定义 3:\(f(x)\) quasiconvex 等价于:定义域为凸集,且 \[ f(y)\le f(x) \Longrightarrow \nabla f^T(x)(y-x)\le0 \] Remarks:该定义实际上是指 \(\nabla f(x)\) 定义了一个 \(R^n\) 空间中的超平面(作为法向量),该超平面就是某一个下水平集的支撑超平面 \[ S_\alpha = \{y| f(y)\le f(x)=\alpha \}\subseteq R^n \] 需要注意的是,前面讲的对于凸函数来说 \(\left[\nabla f^T(x)\ \ -1\right]^T\) 定义了一个 \(R^{n+1}\) 空间中的支撑超平面。注意二者的不同!!!前者是下水平集的支撑超平面,后者是凸函数 surface 的支撑超平面,二者相差一个维度。
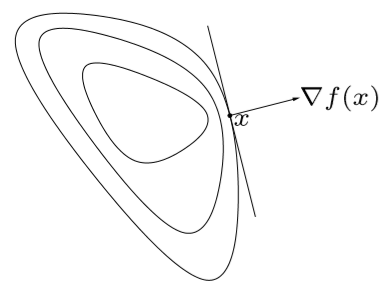
上图中三条封闭曲线代表三个水平集,而 \(\nabla f(x)\) 就是其中一个水平集的支撑超平面。这可以联想梯度下降法(牛顿下山法),想象这是一个山谷,每一条线都是一个等高线,\(\left[\nabla f^T(x)\ \ -1\right]^T\)是山坡地面的法向量,指向空中,而\(\nabla f(x)\)则在这个等高线所在的平面内,且指向山体内部,与等高线相切。。
2.3 二阶条件
对于拟凸函数来说,没有二阶的充分必要条件,有充分条件和必要条件。
必要条件:\(f(x)\) quasiconvex \(\Longrightarrow\) 对任意 \(x\in\text{dom}f,y\in R^n\) \[ \text{if }\quad y^T \nabla f(x)=0 \Longrightarrow y^T\nabla^2f(x)y\ge0 \] 对于一维函数,只需要 \(f'(x)=0 \Longrightarrow f''(x)\ge0\)
充分条件:\(f(x)\) quasiconvex \(\Longleftarrow\) 对任意 \(x\in\text{dom}f,y\in R^n,y\ne0\) \[ \text{if }\quad y^T \nabla f(x)=0 \Longrightarrow y^T\nabla^2f(x)y>0 \] 证明:注意这里对于一维函数 \(f:R\to R\) 较简单,因此可以应用“降维打击”的等价定义进行证明。
3. 拟凸函数的保凸变换
先来复习一下凸函数的保凸变换
- 正权重求和
- 与仿射变换复合
- 最大值/上确界
- 单调凸函数与凸函数的复合
- 下确界
- 透射变换
拟凸函数的也是类似的,主要少了第一个和最后一个,也即拟凸函数的正权重求和不一定是拟凸的,也没有透射变换的定义。
3.1 与仿射变换复合
若 \(f\) 拟凸,则 \(g(x)=f(Ax+b)\) 也是拟凸的
这个也很简单,因为 \(g(x)\) 的下水平集就是 \(f(y)\) 的下水平集外加仿射变换 \(y=Ax+b\),仿射变换不改变凸性。
3.2 最大值/上确界
离散情况:\(f=\max\{\omega_1 f_1,...,\omega_m f_m\},\omega_i\ge0\)
连续情况:\(g(x)=\sup\{w(y)f(x,y),\omega(y)\ge0\}\) 是拟凸的,如果 \(f(\cdot,y)\) 是拟凸的
证明很简单,因为导出函数的下水平集就是多个拟凸函数下水平集的交集,当然也是凸集。
3.3 复合函数
如果 \(g\) 为拟凸函数,且 \(h\) 单调递增,则 \(f=h\circ g\) 是拟凸的
证明的话也可以从下水平集的角度理解。
例:若 \(f\) 是拟凸的,则 \(g(x)=f(Ax+b)\) 是拟凸的,且 \(\tilde{g}(x)=f((Ax+b)/(c^Tx+d))\) 也是拟凸的,其中 \[ \{x|c^Tx+d>0,(Ax+b)/(c^Tx+d)\in\text{dom}f\} \] 原因很简单,\(\tilde{g}(x)\) 的下水平集就是 \(f(y)\) 的下水平集外加一个线性分式变换 \(y=(Ax+b)/(c^Tx+d)\),而线性分式函数也不改变凸性。
3.4 下确界
\(f(x,y)\) 对于 \((x,y)\) 是拟凸的,则 \(g(x)=\inf_{y\in C}f(x,y)\) 是拟凸的
证明可以应用 Jensen 不等式。
Reamrks:这些保凸变换,前三个都可以直接从下水平集的角度来理解和证明,变换后函数的下水平集都是原始函数下水平集外加一个集合保凸变换,最后一个则不太直观,不过也可以由 Jensen 不等式直接导出。看来要理解拟凸函数,还是要多从下水平集的角度来看,并且集合的保凸变换也是很重要的!