凸优化笔记 4:凸函数 Convex Function
1. 凸函数
1.1 凸函数定义
凸函数(convex function)的定义: \[ f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y),\quad \forall x,y\in\text{dom}f,\theta\in[0,1] \] 函数 \(f\) 的扩展函数(extended-value extension) \(\tilde{f}\) 定义为 \[ \tilde{f}(x)=\begin{cases}f(x),&x\in\text{dom}f\\\infty,&x\notin\text{dom}f\end{cases} \] 相当于对原来函数 \(f\) 的定义域进行了扩展。
1.2 常见凸函数
1.2.1 \(R\)
凸函数(convex)
- 仿射函数 \(ax+b\),for any \(a,b\in R\)
- 指数函数 \(e^{ax}\),for any \(a\in R\)
- 幂函数 \(x^\alpha,x\in R_{++}\),for \(\alpha\ge1\) or \(\alpha\le0\)
- 绝对值幂函数 \(\vert x\vert^p,x\in R\),for \(p\ge 1\)
- 负熵 \(x\log x,x\in R_{++}\)
凹函数(concave)
- 仿射函数 \(ax+b\),for any \(a,b\in R\)
- 幂函数 \(x^\alpha,x\in R_{++}\),for \(0\le\alpha\le1\)
- 对数函数 \(\log x,x\in R_{++}\)
1.2.2 \(R^n\)
- 仿射函数 \(a^Tx+b\)
- 范数 \(\Vert x\Vert_p,p\ge 1\)
1.2.3 \(R^{m\times n}\)
- 仿射函数 \(f(X)=\text{tr}(A^TX)+b\)
- 谱范数 \(f(X)=\Vert X\Vert_2=\sigma_{\max}(X)=(\lambda_\max(X^TX))^{1/2}\)
2. 凸函数判定
2.1 “降维打击”
“降维打击”是指对于函数 \(f:R^n\to R\) 限制在某一个方向上观察,若对于任意一个方向上都是凸函数,则 \(f\) 就是凸函数。准确的定义如下。
设 \(f:R^n\to R\),有映射 \(g:R\to R\) \[ g(t)=f(x+tv),\quad \text{dom}\ g=\{t|x+tv\in\text{dom}\ f\} \] 则 \(f\) 为凸函数当且仅当 \(g(t)\) 对任意 \(x\in\text{dom}f,v\in R^n\) 都是凸函数。
例:函数 \(f:S^n\to R\),有 \(f(X)=\log\det X,\text{dom}f=S^n_{++}\) \[ \begin{align}g(t)=\log\det(X+tV)&=\log\det X + \log\det(I+tX^{-1/2}VX^{-1/2})\\&=\log\det X + \sum_{i=1}^n \log(1+t\lambda_i)\end{align} \] 由于 \(g\) 关于 \(t\) 是凹函数,因此 \(f\) 是凹函数。
2.2 一阶条件
函数 \(f\) 为凸函数当且仅当 \[ f(y)\ge f(x)+\nabla f^T(x)(y-x) \quad \forall x,y\in\text{dom}f \] 证明:略。用定义即可。
2.3 二阶条件
函数 \(f\) 为凸函数当且仅当海森矩阵(Hessian matrix)(若二阶可微) \[ \nabla^2 f(x)\succeq0 \quad \forall x\in\text{dom}f \]
可用海森矩阵验证为凸函数的例子
- 二次函数 \(f(x)=(1/2)x^TPx+q^Tx+r\) (with \(P\in S^n\))
- 最小二乘目标函数 \(f(x)=\Vert Ax-b\Vert_2^2\)
- 二次函数 \(f(x,y)=x^2/y\)
- log-sum-exp \(f(x)=\log\sum_k\exp x_k\)
- 几何均值 \(f(x)=(\Pi_k x_k)^{1/n}\) on \(R^n_{++}\)
3. Sublevel set & Epigraph
函数 \(f:R^n\to R\) 的 \(\alpha\) 下水平集(\(\alpha\)-sublevel set) 的定义为 \[ C_\alpha=\{x\in\text{dom}f|f(x)\le\alpha\} \] 凸函数的下水平集也是凸集,但是反之不一定成立。
针对函数 \(f:R^n\to R\) 定义的 epigraph 为 \[ \text{epi}f=\{(x,t)\in R^{n+1}|x\in\text{dom}f,f(x)\le t\} \]
函数 \(f\) 为凸函数当且仅当其 epigraph 为凸集。
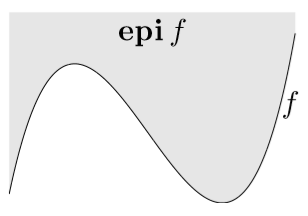
Remarks:对于 epigraph 内的点,有 \[ \begin{align} t\ge f(y)\ge f(x)+\nabla f^T(x)(y-x) \\ \iff \left[\begin{array}{cc}\nabla f^T(x)\\-1\end{array}\right] \left(\left[\begin{array}{cc}y\\t\end{array}\right] - \left[\begin{array}{cc}x\\f(x)\end{array}\right]\right)\le0 \end{align} \] 上面的式子实际上就是找到了一个在 \((x,f(x))\) 处的支撑超平面,法向量即为 \([\begin{array}{cc}\nabla f^T(x) &-1\end{array}]^T\)
4. Jensen's Inequality
对于凸函数 \(f\),有 \[ f(\mathbb{E}z)=\mathbb{E}f(z) \] 证明:离散情况易证,连续情况可以用一阶条件证明。
Lemma:\(f:R^n\to R\) 为凸函数,那么 \(f\) 在任一内点处都连续(连续但不一定可导)。
Remarks:往往绝大部分点都是可微的,但是我们经常会遇到那些不可微的点,比如 ReLU 函数。
