统计推断(一) Hypothesis Test
假设检验
1. Binary Bayesian hypothesis testing
1.0 Problem Setting
- Hypothesis
- Hypothesis space \(\mathcal{H}=\{H_0, H_1\}\)
- Bayesian approach: Model the valid hypothesis as an RV H
- Prior \(P_0 = p_\mathsf{H}(H_0), P_1=p_\mathsf{H}(H_1)=1-P_0\)
- Observation
- Observation space \(\mathcal{Y}\)
- Observation Model \(p_\mathsf{y|H}(\cdot|H_0), p_\mathsf{y|H}(\cdot|H_1)\)
- Decision rule \(f:\mathcal{Y\to H}\)
- Cost function \(C: \mathcal{H\times H} \to
\mathbb{R}\)
- Let \(C_{ij}=C(H_j,H_i), correct hypo is H_j\)
- \(C\) is valid if \(C_{jj}<C_{ij}\)
- Optimum decision rule \(\hat{H}(\cdot) = \arg\min\limits_{f(\cdot)}\mathbb{E}[C(\mathsf{H},f(\mathsf{y}))]\)
1.1 Binary Bayesian hypothesis testing
Theorem: The optimal Bayes' decision takes the form \[ L(\mathsf{y}) \triangleq \frac{p_\mathsf{y|H}(\cdot|H_1)}{p_\mathsf{y|H}(\cdot|H_0)} \overset{H_1} \gtreqless \frac{P_0}{P_1} \frac{C_{10}-C_{00}}{C_{01}-C_{11}} \triangleq \eta \]
Proof: \[ \begin{align} \varphi(f) &=\mathbb{E} [C(H, f(y))] \\ &= \int_{y*} \mathbb{E} [C(H,f(y^*) | \mathsf{y}=y^*)] \\ \end{align} \]
Given \(y^*\)
- if \(f(y^*)=H_0\), \(\mathbb{E}=C_{00}p_{\mathsf{H|y}}(H_0|y^*)+C_{01}p_{\mathsf{H|y}}(H_1|y^*)\)
- if \(f(y^*)=H_1\), \(\mathbb{E}=C_{10}p_{\mathsf{H|y}}(H_0|y^*)+C_{11}p_{\mathsf{H|y}}(H_1|y^*)\)
So \[ \frac{p_\mathsf{H|y}(H_1|y^*)}{p_\mathsf{H|y}(H_0|y^*)} \overset{H_1} \gtreqless \frac{C_{10}-C_{00}}{C_{01}-C_{11}} \]
备注:证明过程中,注意贝叶斯检验为确定性检验,因此对于某个确定的 y,\(f(y)=H_1\) 的概率要么为 0 要么为 1。因此对代价函数求期望时,把 H 看作是随机变量,而把 \(f(y)\) 看作是确定的值来分类讨论
Special cases
- Maximum a posteriori (MAP)
- \(C_{00}=C_{11}=0,C_{01}=C_{10}=1\)
- \(\hat{H}(y)==\arg\max\limits_{H\in\{H_0,H_1\}} p_\mathsf{H|y}(H|y)\)
- Maximum likelihood (ML)
- \(C_{00}=C_{11}=0,C_{01}=C_{10}=1, P_0=P_1=0.5\)
- \(\hat{H}(y)==\arg\max\limits_{H\in\{H_0,H_1\}} p_\mathsf{y|H}(y|H)\)
1.2 Likelyhood Ratio Test
Generally, LRT \[ L(\mathsf{y}) \triangleq \frac{p_\mathsf{y|H}(\cdot|H_1)}{p_\mathsf{y|H}(\cdot|H_0)} \overset{H_1} \gtreqless \eta \]
- Bayesian formulation gives a method of calculating \(\eta\)
- \(L(y)\) is a sufficient statistic for the decision problem
- \(L(y)\) 的可逆函数也是充分统计量
充分统计量
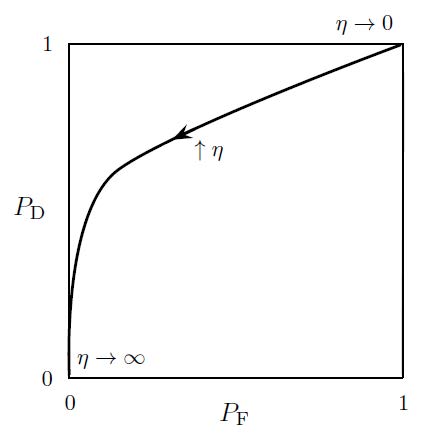
1.3 ROC
- Detection probability \(P_D = P(\hat{H}=H_1 | \mathsf{H}=H_1)\)
- False-alarm probability \(P_F = P(\hat{H}=H_1 | \mathsf{H}=H_0)\)
性质(重要!)
- LRT 的 ROC 曲线是单调不减的
2. Non-Bayesian hypo test
- Non-Bayesian 不需要先验概率或者代价函数
Neyman-Pearson criterion
\[ \max_{\hat{H}(\cdot)}P_D \ \ \ s.t. P_F\le \alpha \]
Theorem(Neyman-Pearson Lemma):NP 准则的最优解由 LRT 得到,其中 \(\eta\) 由以下公式得到 \[ P_F=P(L(y)\ge\eta | \mathsf{H}=H_0) = \alpha \]
Proof:
物理直观:同一个 \(P_F\) 时 LRT 的 \(P_D\) 最大。物理直观来看,LRT 中判决为 H1 的区域中 \(\frac{p(y|H_1)}{p(y|H_0)}\) 都尽可能大,因此 \(P_F\) 相同时 \(P_D\) 可最大化
备注:NP 准则最优解为 LRT,原因是
- 同一个 \(P_F\) 时, LRT 的 \(P_D\) 最大
- LRT 取不同的 \(\eta\) 时,\(P_F\) 越大,则 \(P_D\) 也越大,即 ROC 曲线单调不减
3. Randomized test
3.1 Decision rule
Two deterministic decision rules \(\hat{H'}(\cdot),\hat{H''}(\cdot)\)
Randomized decision rule \(\hat{H}(\cdot)\) by time-sharing \[ \hat{\mathrm{H}}(\cdot)=\left\{\begin{array}{ll}{\hat{H}^{\prime}(\cdot),} & {\text { with probability } p} \\ {\hat{H}^{\prime \prime}(\cdot),} & {\text { with probability } 1-p}\end{array}\right. \]
- Detection prob \(P_D=pP_D'+(1-p)P_D''\)
- False-alarm prob \(P_F=pP_F'+(1-P)P_F''\)
A randomized decision rule is fully described by \(p_{\mathsf{\hat{H}|y}}(H_m|y)\) for m=0,1
3.2 Proposition
Bayesian case: cannot achieve a lower Bayes' risk than the optimum LRT
Proof: Risk for each y is linear in \(p_{\mathrm{H} | \mathbf{y}}\left(H_{0} | \mathbf{y}\right)\), so the minima is achieved at 0 or 1, which degenerate to deterministic decision \[ \begin{align} \varphi(\mathbf{y})&=\sum_{i, j} C_{i j} \mathbb{P}\left(\mathrm{H}=H_{j}, \hat{\mathrm{H}}=H_{i} | \mathbf{y}=\mathbf{y}\right)=\sum_{i, j} C_{i j} p_{\mathrm{\hat H} | y}\left(H_{i} | \mathbf{y}\right) p_{\mathrm{H} | \mathbf{y}}\left(H_{j} | \mathbf{y}\right) \\ &= \Delta(y) + P(\hat H=H_0|y) \frac{P(y|H_0)}{p(y)}P_1(C_{01}-C_{11})(L(y)-\eta) \end{align} \]
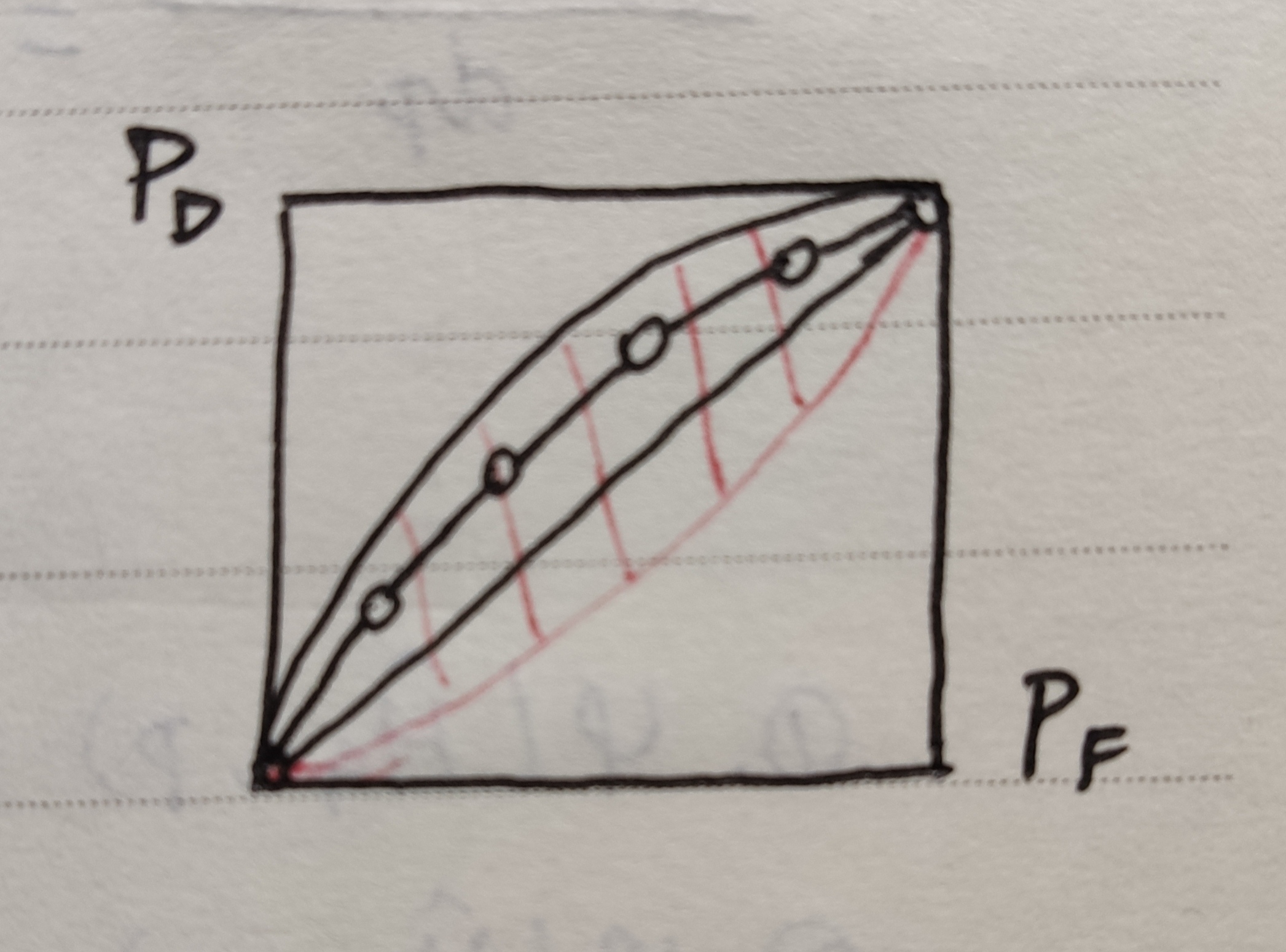
Neyman-Pearson case:
- continuous-valued: For a given \(P_F\) constraint, randomized test cannot achieve a larger \(P_D\) than optimum LRT
- discrete-valued: For a given \(P_F\) constraint, randomized test can achieve a larger \(P_D\) than optimum LRT. Furthermore, the optimum rand test corresponds to simple time-sharing between the two LRTs nearby
3.3 Efficient frontier
Boundary of region of achievable \((P_D,P_F)\) operation points
- continuous-valued: ROC of LRT
- discrete-valued: LRT points and the straight line segments
Facts
- \(P_D \ge P_F\)
- efficient frontier is concave function
- \(\frac{dP_D}{dP_F}=\eta\)
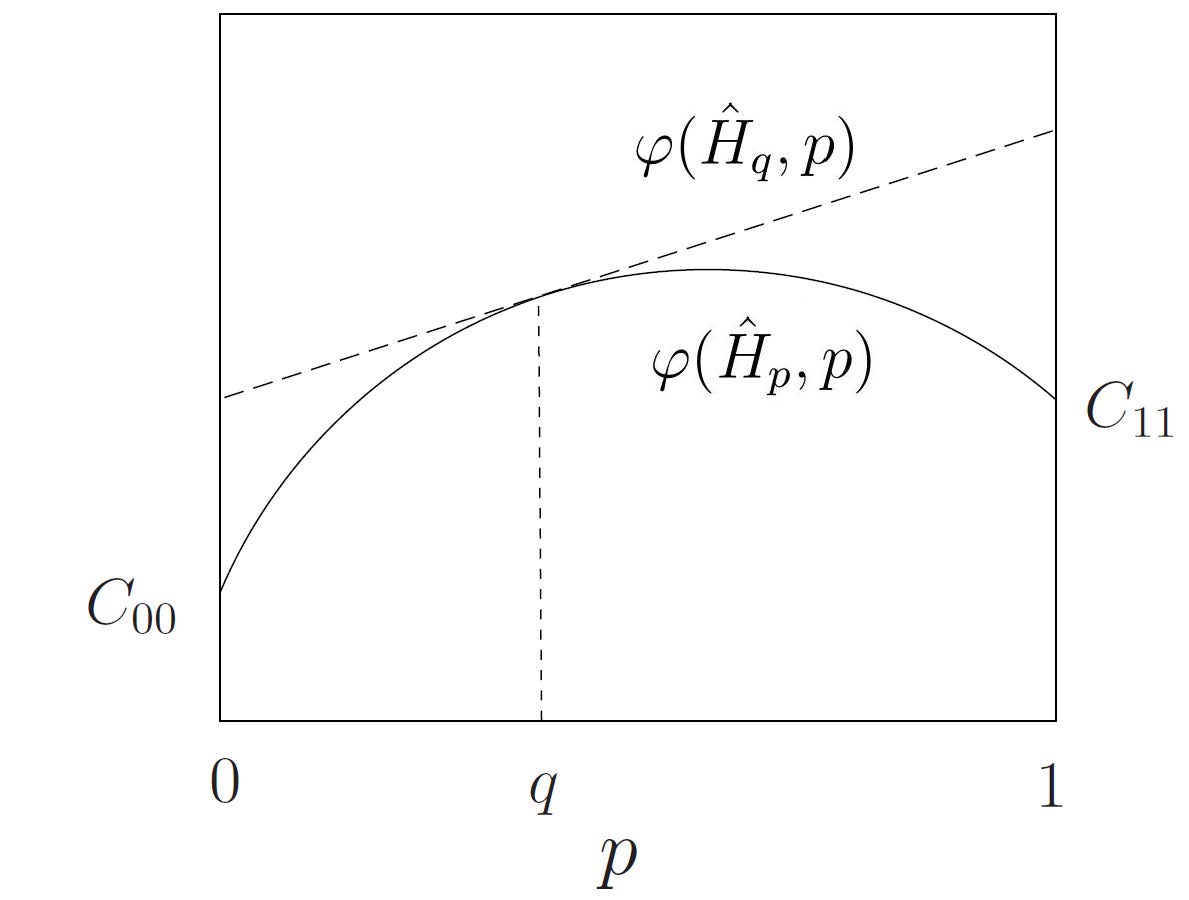
4. Minmax hypo testing
prior: unknown, cost fun: known
4.1 Decision rule
minmax approach \[ \hat H(\cdot)=\arg\min_{f(\cdot)}\max_{p\in[0,1]} \varphi(f,p) \]
optimal decision rule \[ \hat H(\cdot)=\hat{H}_{p_*}(\cdot) \\ p_* = \arg\max_{p\in[0,1]} \varphi(\hat H_p, p) \]
要想证明上面的最优决策,首先引入 mismatch Bayes decision \[ \hat{\mathrm{H}}_q(y)=\left\{ \begin{array}{ll}{H_1,} & {L(y) \ge \frac{1-q}{q}\frac{C_{10}-C_{00}}{C_{01}-C_{11}}} \\ {H_0,} & {otherwise}\end{array}\right. \] 代价函数如下,可得到 \(\varphi(\hat H_q,p)\) 与概率 \(p\) 成线性关系 \[ \varphi(\hat H_q,p)=(1-p)[C_{00}(1-P_F(q))+C_{10}P_F(q)] + p[C_{01}(1-P_D(q))+C_{11}P_D(q)] \]
Lemma: Max-min inequality \[ \max_x\min_y g(x,y) \le \min_y\max_x g(x,y) \] Theorem:
\[ \min_{f(\cdot)}\max_{p\in[0,1]}\varphi(f,p)=\max_{p\in[0,1]}\min_{f(\cdot)}\varphi(f,p) \] Proof of Lemma: Let \(h(x)=\min_y g(x,y)\) \[ \begin{aligned} g(x) &\leq f(x, y), \forall x \forall y \\ \Longrightarrow \max _{x} g(x) & \leq \max _{x} f(x, y), \forall y \\ \Longrightarrow \max _{x} g(x) & \leq \min _{y} \max _{x} f(x, y) \end{aligned} \] Proof of Thm: 先取 \(\forall p_1,p_2 \in [0,1]\),可得到 \[ \varphi(\hat H_{p_1},p_1)=\min_f \varphi(f,p_1) \le \max_p \min_f \varphi(f,p) \le \min_f \max_p \varphi(f, p) \le \max_p \varphi(\hat H_{p_2}, p) \] 由于 \(p_1,p_2\) 任取时上式都成立,因此可以取 \(p_1=p_2=p_*=\arg\max_p \varphi(\hat H_p, p)\)要想证明定理则只需证明 \(\varphi(\hat H_{p_*},p_*)=\max_p \varphi(\hat H_{p_*}, p)\)
由前面可知 \(\varphi(\hat H_q,p)\) 与 \(p\) 成线性关系,因此要证明上式
- 若 \(p_* \in (0,1)\),只需 \(\left.\frac{\partial \varphi\left(\hat{H}_{q^{*}}, p\right)}{\partial p}\right|_{\text {for any } p}=0\),等式自然成立
- 若 \(p_* = 1\),只需 \(\left.\frac{\partial \varphi\left(\hat{H}_{q^{*}}, p\right)}{\partial p}\right|_{\text {for any } p} > 0\),最优解就是 \(p=1\);\(q_*=0\) 同理
根据下面的引理,可以得到最优决策就是 Bayes 决策 \(p_*=\arg\max_p \varphi(\hat H_p, p)\),其中 \(p_*\) 满足 \[ \begin{aligned} 0 &=\frac{\partial \varphi\left(\hat{H}_{p_{*}}, p\right)}{\partial p} \\ &=\left(C_{01}-C_{00}\right)-\left(C_{01}-C_{11}\right) P_{\mathrm{D}}\left(p_{*}\right)-\left(C_{10}-C_{00}\right) P_{\mathrm{F}}\left(p_{*}\right) \end{aligned} \] Lemma: \[ \left.\frac{\mathrm{d} \varphi\left(\hat{H}_{p}, p\right)}{\mathrm{d} p}\right|_{p=q}=\left.\frac{\partial \varphi\left(\hat{H}_{q}, p\right)}{\partial p}\right|_{p=q}=\left.\frac{\partial \varphi\left(\hat{H}_{q}, p\right)}{\partial p}\right|_{\text {for any } p} \]