矩阵分析学习笔记
在网上自学矩阵分析的一些笔记,主要是总结一些结论性的东西,并没有太多证明。对于非数学专业的学生,笔者认为抛开证明的细节,从更加具象的角度理解矩阵可能会有更清晰的理解。
未完待续,更新中 ...
参考资料:知乎专栏
1. 线性代数基础——空间
几个基本的概念
数域:对加减乘除四则基本运算封闭的数集
- 注意:首先数域的概念针对的是数集,不是向量也不是矩阵;其次要求对四则基本运算封闭。
线性空间:需满足以下条件 \[ \begin{alignat}{1} &1)\ \alpha+\beta=\beta+\alpha &5)\ 1 a=\alpha\notag\\ &2)\ (\alpha+\beta)+\gamma=\alpha+(\beta+\gamma) &6)\ k(l \alpha)=(k l) \alpha\notag\\ &3)\ \exists 0 \in V, \forall \alpha \in V, 有 \alpha+0=\alpha &7)\ (k+l) \alpha=k \alpha+l \alpha\notag\\ &4)\ \forall \alpha \in V, \exists \beta \in V, s.t.\ \alpha+\beta=0 \qquad &8)\ k(\alpha+\beta)=k \alpha+l \beta\notag\\ \end{alignat}\notag \]
子空间:
空间的维数:基的个数
平凡子空间:V 空间的子空间只有 0 空间和 V 空间本身
非平凡子空间:除了平凡子空间,其他所有子空间
子空间的直和:\(V_1 \cap V_2=\{0\}\) 时,直和可定义为 \(V_1 \bigoplus V_2\),主要是为了保证分解的唯一性。可以推广到多个子空间 \(V_i (\sum_{j\ne i}V_j) = \{0\}\)
- 注:\(V_1,V_2\) 相互可能不是正交的,比如二维平面中不正交的两个基
酉空间:欧几里得空间推广到复数域
2. 投影
- 变换:线性空间到自身的映射 \(T:V(C)\to V(C)\)
- 线性变换:
- \(T(\alpha+\beta) = T(\alpha)+T(\beta)\)
- \(T(k\alpha) = kT(\alpha)\)
- 投影:\(T\) 是 \(V(C)\) 上的投影, \(\iff T^2=T\)
定理 1:设 \(T\) 是 \(V(C)\) 上的投影,则 \(V(C) = R(T)\bigoplus N(T)\)
定理 2:设 \(V(C) = V_1\bigoplus V_2\),则存在投影 \(T\) 使得 \(R(T)=V_1, N(T)=V_2\)
Remark:根据投影的定义 \(T^2=T\),可以形象理解为降维操作,也即投影过程不可逆,投影一次后即进入值域 \(R(T)\),也即是 \(V(C)\) 的一个低维子空间。
投影矩阵:投影 \(T\) 为线性变换,可以用矩阵 \(A\) 表示

幂等矩阵:满足 \(A^2=A\),有如下性质
- \(A^H\) 与 \((E-A)\) 也是幂等矩阵
- \(A\) 的特征值只有 0 和 1,且可以对角化
- \(rank(A)=tr(A)\)
- \(A(E-A)=(E-A)A\)
- \(Aa = a, \iff a\in R(A)\)
- \(N(A)=R(E-A), R(A)=N(E-A)\)
上面的性质均可由幂等矩阵的性质导出
正交投影:\(\iff R^{\perp}(T) = N(T) \iff A^H=A\)
Remark:
- 实际上对于正交投影 \(A\),可以写成以下形式
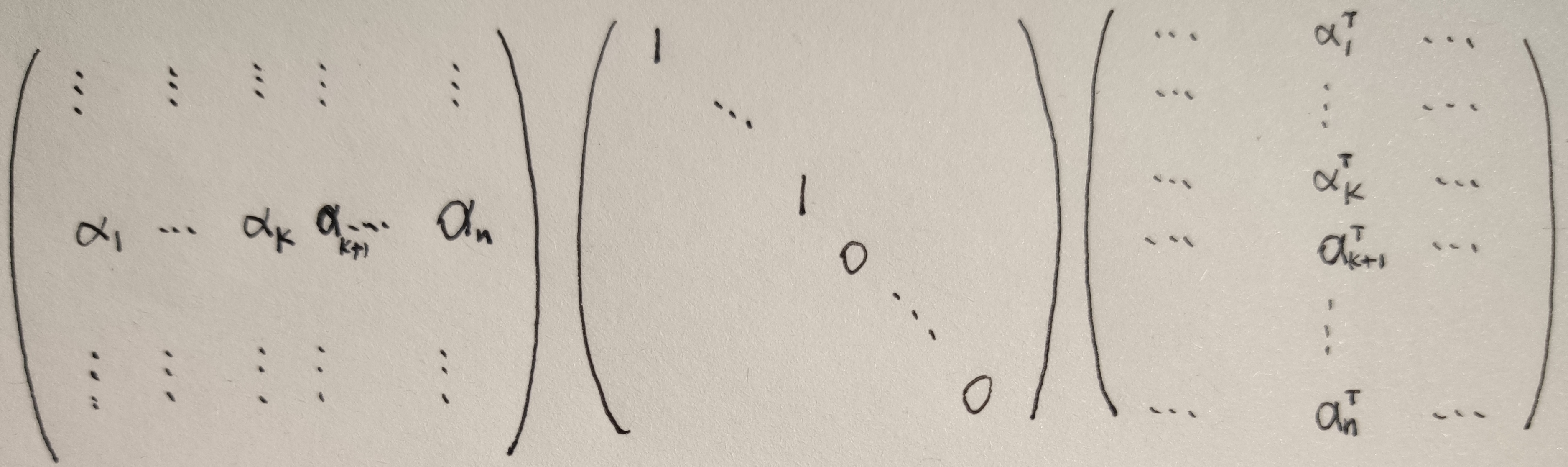
- 是否存在非正交投影呢?非正交投影又是什么形式呢? 只需要将中间的对角阵换成Jordan标准型的形式?
3. Jordan标准型
注:此部分是矩阵论的基本定理之一,非常重要!!!
定理 1:任意 n 阶矩阵 \(A\),一定存在 n 阶可逆矩阵 P 使得 \[ P^{-1} A P=\left(\begin{array}{cccc} {J_{1}} & {} & {} & {} \\ {} & {J_{2}} & {} & {} \\ {} & {} & {\ddots} & {} \\ {} & {} & {} & {J_{k}} \end{array}\right)=J \notag \] 其中 \(J_i\) 为 Jordan 块。有以下几个结论
- Jordan 块的个数是线性无关特征向量的个数
- 矩阵可对角化当且仅当 \(k=n\)
- 对于某个特征值,Jordan 块个数为几何重数,所有 Jordan 块的阶数之和为代数重数(特征值多项式根的阶数即为代数重数,永远有几何重数不大于代数重数)
- 特征值的几何重数不大于代数重数
- 矩阵不同特征值对应的特征向量线性无关
4. 初等矩阵与酉矩阵
4.1 初等变换矩阵
定义:设 \(\boldsymbol{u,v}\in \mathbb{C}^n,\sigma\in \mathbb{C}\),则称 \(E(\boldsymbol{u,v},\sigma)=E-\sigma\boldsymbol{uv}^H\) 为初等变换矩阵
初等变换矩阵性质
- 特征向量
- 若 \(\boldsymbol{u\in v^{\perp}}\),设 \(\boldsymbol{u_1,...,u_{n-1}}\) 是 \(v^\perp\) 的一组基,则 \(E(\boldsymbol{u,v},\sigma)\) 的一组线性无关的特征向量为 \(\boldsymbol{u_1,...,u_{n-1}}\)
- 若 \(\boldsymbol{u\notin v^{\perp}}\),设 \(\boldsymbol{u_1,...,u_{n-1}}\) 是 \(v^\perp\) 的一组基,则 \(E(\boldsymbol{u,v},\sigma)\) 的一组线性无关的特征向量为 \(\boldsymbol{u,u_1,...,u_{n-1}}\)
- 特征值 \(\lambda(E(\boldsymbol{u,v},\sigma))=\{1,...,1,1-\sigma v^H u\}\)
- 行列式 \(det(E(\boldsymbol{u,v},\sigma))=1-\sigma v^H u\)
- 逆矩阵 \(E(u, v, \sigma)^{-1}=E\left(u, v, \frac{\sigma}{\sigma v^{H} u-1}\right),\left(1-\sigma v^{H} u \neq 0\right)\)
- 非零向量 \(\boldsymbol{a,b}\in\mathbb{C}^n\),存在 \(\boldsymbol{u,v},\sigma\) 使得 \(E(u, v, \sigma) a=b,\left(\sigma u=\frac{a-b}{v^{H} a}\right)\)
Remarks
- 前两个性质可以根据 \(u,v\) 的垂直关系直观想象。当 \(u\perp v\) 时,此时 \(E\) 对于特征值 \(1\) 的代数重数为 \(n\),而几何重数为 \(n-1\)(注意此时出现了代数重数大于几何重数的情况!);否则,\(E\) 对于特征值 \(1\) 的代数重数和几何重数为 \(n-1\),且有另一个特征值 \(1-\sigma v^H u\)
- 特征向量
所有初等变换可以用上述定义表示
- 置换 \({E_{i j}=E-\left(e_{i}-e_{j}\right)\left(e_{i}-e_{j}\right)^{T}=E\left(e_{i}-e_{j}, e_{i}-e_{j}, 1\right)}\)
- 相消 \({E_{i j}(k)=E+k e_{j} e_{i}^{T}=E\left(e_{j}, e_{i},-k\right)}\)
- 数乘 \({E_{i}(k)=E-(1-k) e_{i} e_{i}^{T}=E\left(e_{i}, e_{i}, 1-k\right)}\)
4.2 初等酉矩阵
定义:设 \(\boldsymbol{u}\in \mathbb{C}^n\) 且 \(u^H u =1\),则称 \(H(U)=E(\boldsymbol{u,U},2)=E-2\boldsymbol{uu}^H\) 为初等酉矩阵,或者Householder矩阵
- Householder变换性质
- \(H^H=H=H^{-1}\)
- \(H(\boldsymbol{u})(\boldsymbol{a}+r\boldsymbol{u})=\boldsymbol{a}-r\boldsymbol{u}, \forall a\in v^\perp, r\in\mathbb{C}\)(镜像变换)
- 范数不变性:\(||Hx||=||x||\)
- 保持随机向量的协方差
- 可用于数值算法构造正交基
4.3 酉变换
- 酉变换与酉矩阵
- 保持内积不变
- 保持长度不变
- 保持夹角不变
- 保持形状不变
- 内积的定义,比如连续区间中对连续函数的定义
5. 欧氏空间中的度量(?)
内积:满足 4 条性质
- \((x,x)\ge0,且(x,x)=0\iff x=0\)
- \((x,y)=\overline{(y,x)},\forall x,y\in V(P)\)
- \((\lambda x,y)=\bar{\lambda}(x,y),\forall \lambda\in P,\forall x,y\in V(P)\)
- \((x+y,z)=(x,z)+(y,z),\forall x,y,z\in V(P)\)
线性流形:\(P=r_{0}+V_{1}=\left\{r_{0}+\alpha | \alpha \in V_{1}\right\}\)
- 实际上就是将子空间进行平移
n 维空间中的体积
- \(V(\alpha_1)=||\alpha_1||\)
- \(V\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}\right)=V\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n-1}\right) \bullet h_{n}\),其中 \(h_n\) 是 \(\alpha_n\) 到 \(L(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n-1})\) 的距离
Gram 行列式 \[ G\left(\alpha_{1}, \cdots, \alpha_{k}\right)=\left| \begin{array}{cccc} {\left(\alpha_{1}, \alpha_{1}\right)} & {\left(\alpha_{1}, \alpha_{2}\right)} & {\cdots} & {\left(\alpha_{1}, \alpha_{k}\right)} \\ {\left(\alpha_{2}, \alpha_{1}\right)} & {\left(\alpha_{2}, \alpha_{2}\right)} & {\cdots} & {\left(\alpha_{2}, \alpha_{k}\right)} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {\left(\alpha_{k}, \alpha_{1}\right)} & {\left(\alpha_{k}, \alpha_{2}\right)} & {\cdots} & {\left(\alpha_{k}, \alpha_{k}\right)} \end{array}\right|\notag \]
将线性无关向量组 \(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}\) 正交化之后,Gram 行列式不变,即 \(G\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{k}\right)=G\left(\beta_{1}, \beta_{2}, \cdots, \beta_{k}\right)\)
体积 \(V\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}\right)=\sqrt{G\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}\right)}\)
定理 1:设 \(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{k}\) 是 \(V_1\) 的一组基,向量 \(\alpha\) 到流形 \(P=\alpha_0+V_1\) 的距离为 \(d^{2}=\frac{G\left(\alpha_{1}, \cdots, \alpha_{k}, \alpha-\alpha_{0}\right)}{G\left(\alpha_{1}, \cdots, \alpha_{k},\right)}\)
定理 2:线性流形 \(P_1=\alpha_0+V_1\) 和 \(P_2=\alpha_0+V_1\) 之间的距离等于 \(\alpha_1-\alpha_2\) 关于线性子空间 \(V=V_1+V_2\) 的正交分量长度
6. Kronecker积
- 性质
- \(E_m\bigotimes E_n = E_{mn}\)
7. 范数
7.1 向量范数
- 范数:刻画向量大小的度量,需要满足以下三条性质
- 正定性:\(||x||\ge0,且||x||=0\iff x=0\)
- 齐次性:\(||\lambda x||=|\lambda|\cdot ||x||,\lambda\in R,x\in C^n\)
- 三角不等式:\(||x+y||\le ||x||+||y||,\forall x,y\in C^n\)
- 范数与内积的关系是什么?
- 导出性质
- \(||0||=0\)
- \(x\ne0时,||\frac{1}{||x||}x||=1\)
- \(||-x||=||x||,\forall x\in C^n\)
- \(\vert \Vert x\Vert-\Vert y\Vert \vert \le \Vert x-y \Vert\)
- 常用范数
- 1范数:\(\|x\|_{1}=\sum_{i=1}^{n}\left|x_{i}\right|\)
- 2范数:\(\|x\|_{2}=\left(\sum_{i=1}^{n}\left|x_{i}\right|^{2}\right)^{1 / 2}\)
- \(\infty\)范数:\(\|x\|_{\infty}=\max _{1 \leq i \leq n}\left|x_{i}\right|\)
- p范数(Holder范数):\(\|x\|_{p}=\left(\sum_{i=1}^{n}\left|x_{i}\right|^{p}\right)^{1
/ p} \quad 1 \leq p<\infty\)
- p可取正整数
- 可验证满足三角不等式,需要用到Young不等式和Holder不等式
- 向量序列的收敛性
- 向量范数的等价性
 等价性表示不同范数的量级是相同的,只差一个系数
等价性表示不同范数的量级是相同的,只差一个系数- 定理:\(V(P)\) 上的任意两个向量范数均等价
- 范数等价保证了向量序列的收敛性与范数选取无关。无穷范数收敛,其他范数一定收敛。其他范数收敛,无穷范数一定收敛。
7.2 矩阵范数
矩阵可以转化为向量表示
矩阵范数:\(A\in P^{m\times n}\),需满足以下条件
- 正定性:\(||A||\ge0,且||A||=0\iff A=0\)
- 齐次性:\(||\lambda A||=|\lambda|\cdot ||A||,\lambda\in R,A\in P^{m\times n}\)
- 三角不等式:\(||A+B||\le ||A||+||B||,\forall A,B\in P^{m\times n}\)
- 相容性:\(\Vert AB \Vert \le \Vert A\Vert\cdot \Vert B\Vert\)
Remarks:这里相容性的定义目的是什么呢?为了放缩方便?
例如
- (自相容)\(\|A\|_{m_{1}}=\sum_{j=1}^{n} \sum_{i=1}^{m}\left|a_{i j}\right|\)
- (不相容)\(\|A\|_{m_{\infty}}=\max _{i, j}\left\{\left|a_{i j}\right|\right\} \quad 1 \leq i \leq m \quad 1 \leq j \leq n\)
- (自相容)Frobenius范数:\(\|A\|_{m_{2}}=\left(\sum_{j=1}^{n}
\sum_{i=1}^{m}\left|a_{i j}\right|^{2}\right)^{\frac{1}{2}}\)
- \(\|\boldsymbol{A}\|_{m_{2}}^{2}=\operatorname{tr}\left(\boldsymbol{A}^{\boldsymbol{H}} \boldsymbol{A}\right)=\sum_{i=1}^{n} \lambda_{i}\left(\boldsymbol{A}^{\boldsymbol{H}} \boldsymbol{A}\right)\)
- 对任意酉矩阵\(U,V\),\(\|\boldsymbol{A}\|_{m_{2}}^{2}=\left\|\boldsymbol{U}^{\boldsymbol{H}} \boldsymbol{A} \boldsymbol{V}\right\|_{m_{2}}^{2}=\left\|\boldsymbol{U} \boldsymbol{A} \boldsymbol{V}^{\boldsymbol{H}}\right\|_{m_{2}}^{2}\)
7.3 算子范数
向量范数与矩阵范数的相容性:\(\|A x\|_{m} \leq\|A\|_{m}\|x\|_{m}\) 是否成立
- 定义:设 \(\|\cdot\|_a\) 是 \(P^n\) 上的向量范数,\(\|\cdot\|_m\) 是 \(P^{n\times n}\) 上的矩阵范数,且 \[ \|A x\|_{a} \leq\|A\|_{m}\|x\|_{a}\notag \] 则称 \(\|\cdot\|_m\) 为与向量范数 \(\|\cdot\|_a\) 相容的矩阵范数
算子范数
设 \(\|\cdot\|_a\) 是 \(P^n\) 上的向量范数,\(A\in P^{n\times n}\),则 \[ \|\boldsymbol{A}\|_{a}=\underset{\boldsymbol{x} \neq \boldsymbol{\theta}}{\max } \frac{\|\boldsymbol{A} \boldsymbol{x}\|_{a}}{\|\boldsymbol{x}\|_{a}}\left(=\max _{\|u\|_{a}=1}\|A u\|_{a}\right) \notag \] 是与向量范数 \(\|\cdot\|_a\) 相容的矩阵范数
推论:算子范数也是相容的矩阵范数,即 \(\|AB\|_a\le\|A\|_a\|B\|_a\)
常用算子范数
- 极大列和范数:\(\|\boldsymbol{A}\|_{\mathbf{1}}=\mathbf{m}_{\boldsymbol{j}} \mathbf{x}\left(\sum_{\boldsymbol{i}=1}^{\boldsymbol{n}}\left|\boldsymbol{a}_{i j}\right|\right)\)
- 极大行和范数:\(\|A\|_{\infty}=\max _{i}\left(\sum_{j=1}^{n}\left|a_{i j}\right|\right)\)
- 谱范数:\(\|\boldsymbol{A}\|_{2}=\sqrt{r\left(\boldsymbol{A}^{\boldsymbol{H}}
\boldsymbol{A}\right)}\)
- 谱半径:\(r(A)=\max _{i}\left|\lambda_{i}\right|\)
- \(\|A\|_{2}=\left\|A^{H}\right\|_{2}=\left\|A^{T}\right\|_{2}=\|\bar{A}\|_{2}\)
- \(\left\|A^{H} A\right\|_{2}=\left\|A A^{H}\right\|_{2}=\|A\|_{2}^{2}\)
- 对任意酉矩阵\(U,V\),\(\|\boldsymbol{U} \boldsymbol{A}\|_{2}=\|\boldsymbol{A} \boldsymbol{V}\|_{2}=\|\boldsymbol{U} \boldsymbol{A} \boldsymbol{V}\|_{2}=\|\boldsymbol{A}\|_{2}\)
定理
- \(\|\boldsymbol{A}\|_{2}=\max _{\|x\|_{2}=\|y\|_{2}=\mathbf{1}}\left|\boldsymbol{y}^{\boldsymbol{H}} \boldsymbol{A} \boldsymbol{x}\right|\)
- \(\|\boldsymbol{A}\|_{2}^{2} \leq\|\boldsymbol{A}\|_{1}\|\boldsymbol{A}\|_{\infty}\)
8. 矩阵分解
8.1 三角分解
- 三角矩阵
- 逆矩阵仍然是三角矩阵
- 三角矩阵的积仍是三角矩阵
定理(LU分解):设 \(A\in C^{n\times n}\),则 \(A\) 可唯一的分解为 \[ A=U_1 R \notag \] 其中 \(U_1\) 为酉矩阵,\(R\) 为正线上三角矩阵;或者 A 可以唯一的分解为 \[ A = L U_2 \notag \] 其中 \(U_2\) 为酉矩阵,\(L\) 为正线下三角矩阵。
推论 1:对于实数域,则有类似的 QR分解
推论 2.1:对于实对称矩阵,存在唯一上三角实矩阵 \[ A = R^T R \notag \] 推论 2.2:正定 Hermite 矩阵,存在唯一上三角复矩阵 \[ A = R^H R \notag \]
- 任意矩阵的三角分解(非方阵)
8.2 谱分解
- 单纯矩阵:代数重数等于几何重数
定理:设 \(A\in C^{n\times n}\) 是单纯矩阵,则 \(A\) 可以分解为一系列幂等矩阵 \(A_i\) 的加权和 \[ A = \sum_{i=1}^n \lambda_i A_i \notag \] 其中 \(\lambda_i\) 是 \(A\) 的特征值
证明:由单纯矩阵可知 \[ A=P\Lambda P^{-1}=\left(v_{1}, v_{2}, \cdots, v_{n}\right)\left[\begin{array}{cccc}{\lambda_{1}} & {0} & {\cdots} & {0} \\{0} & {\lambda_{2}} & {\cdots} & {0} \\{\cdots} & {\cdots} & {\cdots} & {\cdots} \\{0} & {0} & {\cdots} & {\lambda_{n}}\end{array}\right]\left(\begin{array}{c}{\omega_{1}^{T}} \\{\omega_{2}^{T}} \\{\vdots} \\{\omega_{n}^{T}}\end{array}\right) \notag \] 取 \(A_i = v_i w_i^T\),\(A_i\) 的性质:
- 幂等性:\(A_i^2=A_i\)
- 分离性:\(A_i A_j=0(i\ne0)\)
- 可加性:\(\sum_{i=1}^n A_i = E_n\)
Remarks
这里的幂等矩阵 \(A_i\) 可以看作是正交基的概念
由前面投影矩阵的定义可知,每一个 \(A_i\) 都是一个投影矩阵,将任意一个向量 \(x\) 投影到 \(v_i\) 张成的子空间 \(L(v_i)\) 上。因此上面的幂等矩阵分解实际上可以理解为“特征空间分解”(笔者瞎想的名词),如何理解呢?把每个 \(A_i\) 看作是矩阵 \(A\) 的一个特征子空间(的投影基),\(Ax\) 实际上就是把 \(x\) 投影到各个特征子空间中,然后根据对应的特征值进行伸缩,最后再合成一个作用后的向量,即表示 \(A\) 对 \(x\) 的线性变换。
定理:设 \(A\in C^{n\times n}\),有 \(k\) 个相异的特征值 \(\lambda_i(i=1,...,k)\),则 \(A\) 是单纯矩阵的充要条件是,存在 \(k\) 个矩阵矩阵 \(A_i\) 满足
- \(A_{i} A_{j}=\left\{\begin{array}{ll}{A_{i}} & {i=j} \\ {0} & {i \neq j}\end{array}\right.\)
- \(\sum_{i=1}^k A_i = E_n\)
- \(A = \sum_{i=1}^k \lambda_i A_i\)
- 正规矩阵:满足 \(A^HA=AA^H\) 的矩阵
引理:设 \(A\) 为正规矩阵,\(A\) 与 \(B\) 酉相似,则 \(B\) 为正规矩阵
定理:任意矩阵 \(A\in C^{n\times n}\),存在酉矩阵 \(U\) 使得 \[ A=URU^H \notag \] 其中 \(R\) 为上三角矩阵且主对角线元素为 \(A\) 的特征值
引理:设 \(A\) 为正规矩阵且为三角矩阵,则 \(A\) 为对角矩阵
Remarks:
任意矩阵 \(A\) 都与三角阵 \(R\) 酉相似,因此若矩阵 \(A\) 为正规阵,则 \(R\) 既是正规阵,又是三角阵,则一定是对角阵。
因此,正规阵一定可以对角化,由下面的定理可知,可以酉对角化的矩阵一定是正规矩阵。
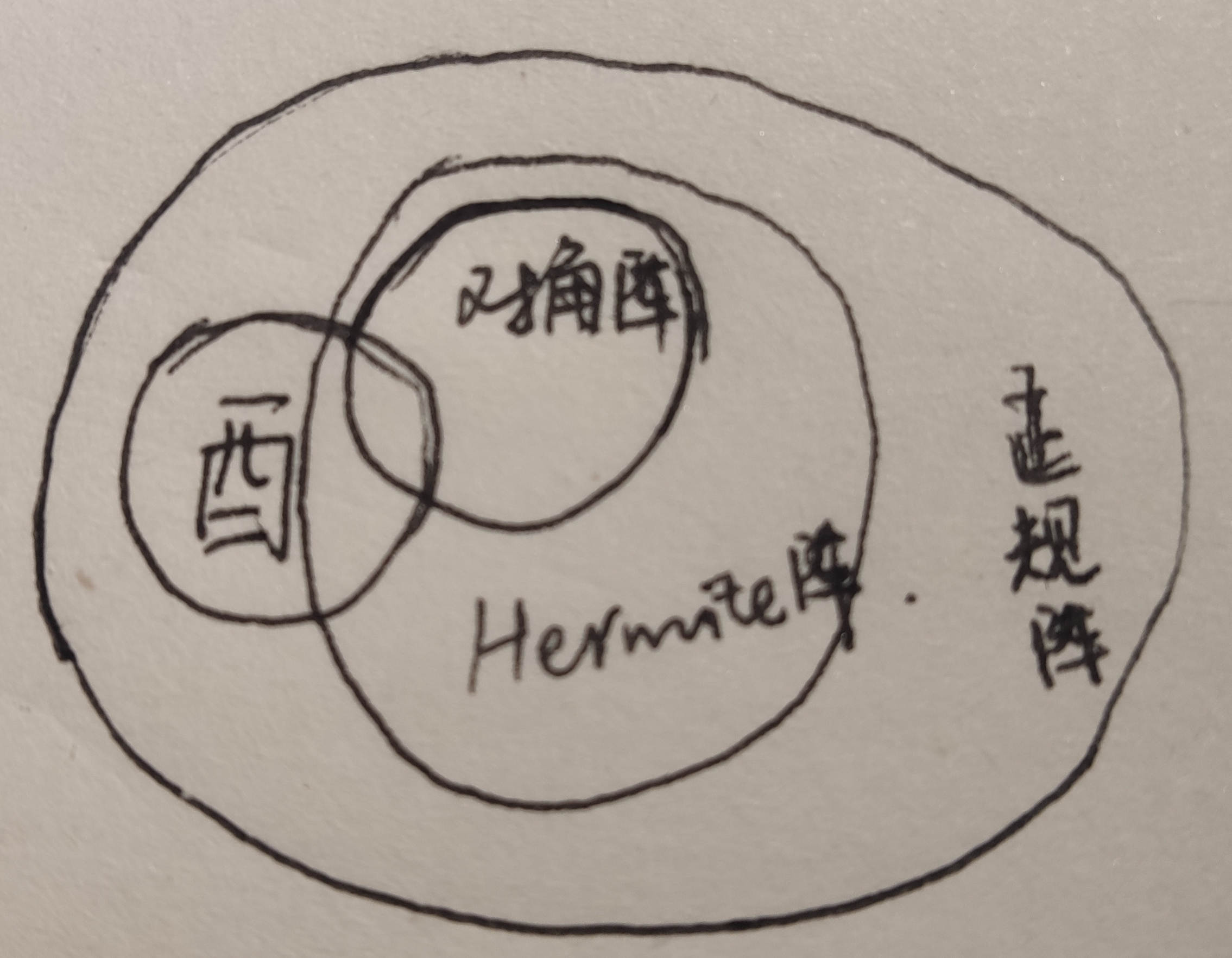
这与普通的可对角化矩阵的区别是什么呢?普通矩阵可对角化的充要条件是代数重数等于几何重数,也即只需要 n 个线性无关的特征向量即可(\(A=PJP^{-1}\))。而正规矩阵则要求所有特征向量正交(\(A=U\Lambda U^H\))!
Remarks
那么正定矩阵与正规矩阵的区别是什么呢?先看正定矩阵的定义:特征值全部为正数。区别很明显了,一个是从特征值角度,另一个是从特征向量角度,牢记这一点就不会弄混两者了。
凡是具有 \(A^HA\) 形式的矩阵,既是正规矩阵,又是正定矩阵!
定理:\(A\) 为正规矩阵的充要条件是存在酉矩阵 \(U\) 使 \[ A = U \text{diag}(\lambda_1,...,\lambda_n)U^H \notag \] 其中 \(\lambda_i\) 是 \(A\) 的特征值
定理:\(A\) 有 \(k\) 个相异特征值,则 \(A\) 是正规矩阵的充要条件是存在 \(k\) 个矩阵 \(A_i\) 满足
- \(A_{i} A_{j}=\left\{\begin{array}{ll}{A_{i}} & {i=j} \\ {0} & {i \neq j}\end{array}\right.\)
- \(\sum_{i=1}^k A_i = E_n\)
- \(A = \sum_{i=1}^k \lambda_i A_i\)
- \(A_i^H = A_i(i=1,...,k)\)
8.3 最大秩分解
- 定理:设 \(A\in
C^{m\times n}_r\),则存在矩阵 \(B\in
C^{m\times r}_r, D\in C^{r\times n}_r\),使得 \(A=BD\)
- 注:可以理解为 \(B\) 取出了 \(r\) 线性无关的列向量,或者 \(D\) 取出了 \(r\) 个线性无关的行向量
- \((B^HB)^{-1}B^HB=E_r\),可以用于求 \(B\) 的左逆,\(D\) 同理
8.4 奇异值分解
- 奇异值:设 \(A\in C^{m\times n}_r\),\(A^HA\) 的特征值为 \(\lambda_{1} \geq \lambda_{2} \geq \cdots \geq \lambda_{r}>\lambda_{r+1}=\cdots=\lambda_{n}=\mathbf{0}\),则称 \(\sigma_{i}=\sqrt{\lambda_{i}}(i=1,2, \cdots, r)\) 为 \(A\) 的正奇异值(实际上就相当于 A 的“绝对特征值”)
- 定理:设 \(A\in
C^{m\times n}_r\),则有
- \(rank(A)=rank(A^HA)=rank(AA^H)\)
- \(A^HA,AA^H\) 的特征值均为非负实数
- \(A^HA,AA^H\) 的特征值相同
- 酉等价:\(A,B\in C^{m\times n}\),存在酉矩阵 \(U,V\) 使得 \(A=UBV\)
- 定理:若 \(A,B\) 酉等价,则它们有相同的奇异值
定理:设 \(A\in C^{m\times n}_r\),\(\sigma_1,...,\sigma_r\) 是 \(A\) 的 \(r\) 个奇异值,则存在酉矩阵 \(U\in C^{m\times m},V\in C{n\times n}\),使得 \[ A=U\left[\begin{array}{ll}{D} & {0} \\ {0} & {0}\end{array}\right] V \notag \] 其中 \(\boldsymbol{D}=\operatorname{diag}\left(\delta_{1}, \delta_{2}, \cdots, \delta_{r}\right),\left|\delta_{i}\right|=\sigma_{i}\)
9. 特征值估计
9.1 几个不等式
- 定理 1(Schur 不等式):设 \(A\in C^{n\times n}\) 的特征值为 \(\lambda_1,...,\lambda_n\),则 \(\sum_{i=1}^{n}\left|\lambda_{i}\right|^{2} \leq \sum_{i=1}^{n} \sum_{j=1}^{n}\left|a_{i j}\right|^{2}=\|A\|_{F}^{2}\),等号成立当且仅当 \(A\) 为正规矩阵
- 定理 2(Hirsch):设 \(A\in
C^{n\times n}\),记 \(B=\frac{A+A^H}{2},C=\frac{A-A^H}{2}\),\(A,B,C\) 特征值分别为 \(\{\lambda_i\},\{\mu_i\},\{i\gamma_i\}\),均从大到小排列。则有
- \(\left|\lambda_{i}\right| \leq n \max _{i, j}\left|a_{i j}\right|\)
- \(\left|\mathbf{R e} \lambda_{i}\right| \leq n \max _{i, j}\left|b_{i j}\right|\)
- \(\left|\mathbf{I m} \lambda_{i}\right| \leq \boldsymbol{n} \max _{i, j}\left|\boldsymbol{c}_{i j}\right|\)
- 定理 3(Bendixson):设 \(A\in R^{n\times n}\),则 \(A\) 的任一特征值满足 \(\left|\mathbf{I m} \lambda_{i}\right| \leq \sqrt{\frac{n(n-1)}{2}} \max _{i, j}\left|c_{i j}\right|\)
9.2 盖尔圆盘定理
- 定义 1:设 \(A\in
C^{n\times n}\)
- 行盖尔圆盘:\(S_{i}=\left\{z \in C:\left|z-a_{i i}\right| \leq R_{i}=\sum_{j \neq i}\left|a_{i j}\right|\right\}\)
- 列盖尔圆盘:\(G_{i}=\left\{z \in C:\left|z-a_{i i}\right| \leq C_{i}=\sum_{j \neq i}\left|a_{j i}\right|\right\}\)
定理 1(圆盘定理):设 \(A\in C^{n\times n}\),则 \(A\) 的任一特征值 \[ \lambda_{i} \in \boldsymbol{S}=\bigcup_{j=1}^{n} \boldsymbol{S}_{j} \quad(\boldsymbol{i}=\mathbf{1}, 2, \cdots, \boldsymbol{n}) \notag \] 类似的,有 \[ \lambda_{i} \in \left(\bigcup_{j=1}^{n} \boldsymbol{S}_{j}\right) \bigcap \left(\bigcup_{j=1}^{n} \boldsymbol{G}_{j}\right) \quad(\boldsymbol{i}=\mathbf{1}, 2, \cdots, \boldsymbol{n}) \notag \] 定理 2:设 \(n\) 阶方阵 \(A\) 的 \(n\) 个盖尔圆盘中有 \(k\) 个圆盘的并形成一个连通区域 \(G\)(圆盘相切也算连通),且它与余下的 \(n-k\) 个圆盘都不相交,则在该区域中恰好有 \(A\) 的 \(k\) 个特征值
证明:取 \(A_{\varepsilon}=D+\varepsilon B,\ \varepsilon \in[0,1]\),而 \(A_\varepsilon\) 的特征值 \(\lambda_i(A_\varepsilon) = \lambda_i(\varepsilon)\) 时关于 \(\varepsilon\) 的连续函数,在圆盘随着 \(\varepsilon\) 扩大过程中,特征值一直都处于圆盘内部
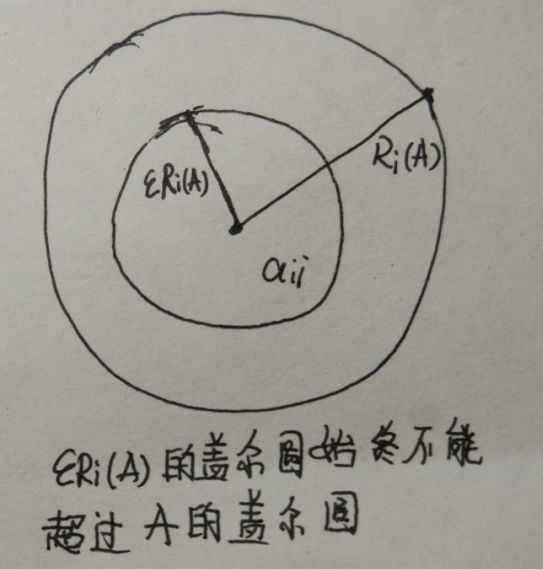
推论 1:设 \(n\) 阶方阵 \(A\) 的 \(n\) 个盖尔圆盘两两互不相交,则 \(A\) 相似于对角阵
推论 2:设 \(n\) 阶实矩阵 \(A\) 的 \(n\) 个盖尔圆盘两两互不相交,则 \(A\) 的特征值全部为实数
改进:可以取 \(D=diag(p_1,...,p_n),\ \ p_i>0\),则有 \(D^{-1}AD\) 与 \(A\) 相似,因此他们有相同的特征值,可以用 \(D^{-1}AD\) 的特征值来估计 \(A\)。此时可以将某些盖尔圆变小,但是代价就是其他盖尔圆会变大。
- 行对角占优:\(\left|a_{ii}\right| \geq R_{i}=\sum_{j=1, j \ne i}^{n}\left|a_{i j}\right| \quad(i=1,2, \cdots, n)\)
- 列对角占优:\(\left|a_{ii}\right| \geq C_{i}=\sum_{j=1, j \ne i}^{n}\left|a_{ji}\right| \quad(i=1,2, \cdots, n)\)
定理 3:设 \(A\in C^{n\times n}\) 严格行对角占优,则
- \(A\) 可逆
- 若 \(A\) 所有主对角元都为正数,则 \(A\) 的特征值都有正实部
- 若 \(A\) 为 Hermite 矩阵,且所有主对角元都为正数,则 \(A\) 的特征值都为正数
9.3 Hermite矩阵特征值的变分特性
因为Hermite矩阵 \(A\in C^{n\times n}\) 的特征值均为实数,所以可以把他们记作(按照大小进行排序): \[ \lambda_{\min }=\lambda_{n} \leq \lambda_{n-1} \ldots \leq \lambda_{2} \leq \lambda_{1}=\lambda_{\max } \notag \]
- Rayleigh 商:\(R(x)=\frac{x^{H} A x}{x^{H} x} \quad x \neq
0\)
- \(\lambda_{n} x^{H} x \leq x^{H} A x \leq \lambda_{1} x^{H} x \quad\left(\forall x \in C^{n}\right)\)
- \(\lambda_{\max }=\lambda_{1}=\max _{x \neq 0} R(x)=\max _{x^{H}} x^{H} A x\)
- \(\lambda_{\min }=\lambda_{n}=\min _{x \neq 0} R(x)=\min _{x^{H} x=1} x^{H} A x\)
- 定理(Courant-Fischer):设特征值 \(\lambda_1 \le \lambda_2 \le \cdots \le
\lambda_n\),则
- \(\begin{array}{ccc}{\min } & {\max } & {R(x)=\lambda_{k}} \\ {\omega_{1}, \omega_{2}, \cdots, \omega_{n-k} \in C^{n}} & {x \neq 0, x \in C^{n} \atop {x \perp \omega_{1}, \omega_{2}, \cdots, \omega_{n-k}}} & {} \end{array}\)
- \(\begin{array}{ccc}{\max } & {\min } & {R(x)=\lambda_{k}} \\ {\omega_{1}, \omega_{2}, \cdots, \omega_{n-k} \in C^{n}} & {x \neq 0, x \in C^{n} \atop {x \perp \omega_{1}, \omega_{2}, \cdots, \omega_{n-k}}} & {} \end{array}\)
- 定理(Weyl):\(\lambda_k(A)+\lambda_n(B)\le\lambda_k(A+B)\le\lambda_k(A)+\lambda_1(B)\)
10. 矩阵分析
10.1 矩阵序列与矩阵级数
- 矩阵序列
- 定理:设 \(\Vert\cdot\Vert\) 是 \(C^{m\times n}\) 上的任一矩阵范数,矩阵序列 \(\{A^{(k)}\}\) 收敛于 \(A\) 的充要条件是 \(\lim _{k \rightarrow+\infty}\left\|A^{(k)}-A\right\|=0\)
- 定理:设 \(\lim _{k
\rightarrow+\infty} A^{(k)}=A, \lim _{k \rightarrow+\infty} B^{(k)}=B .
\alpha, \beta \in C\),则
- \(\lim _{k \rightarrow+\infty}\left(\alpha A^{(k)}+\beta B^{(k)}\right)=\alpha A+\beta B\)
- \(\lim _{k \rightarrow+\infty} A^{(k)} B^{(k)}=A B\)
- 当 \(A^{(k)}\) 与 \(A\) 都可逆时,\(\lim _{k \rightarrow+\infty}\left(A^{(k)}\right)^{-1}=A^{-1}\)
- 收敛矩阵:设 \(A\in
C^{n\times n}\),若 \(\lim _{k
\rightarrow \infty} A^{k}=0\),则称 \(A\) 为收敛矩阵
- 定理:设 \(A\in C^{n\times n}\),则 \(A\) 为收敛矩阵的充要条件是 \(r(A)<1\)
- 矩阵级数:\(\sum_{k=1}^{\infty}
A^{(k)}=A^{(1)}+A^{(2)}+\cdots+A^{(k)}+\cdots\),称 \(\boldsymbol{S}^{(\boldsymbol{N})}=\sum_{\boldsymbol{k}=1}^{\boldsymbol{N}}
\boldsymbol{A}^{(\boldsymbol{k})}\) 为矩阵级数的部分和,若 \(\lim _{N \rightarrow \infty} S^{(N)}=S\)
则称级数收敛
- 定理:在 \(C^{n\times n}\) 中,\(\sum_{k=1}^{\infty} A^{(k)}\) 绝对收敛的充要条件是正项级数 \(\sum_{k=1}^{\infty}\left\|A^{(k)}\right\|\) 收敛
- 定理:方阵 \(A\) 的 Neumann 级数 \(\sum_{k=0}^{\infty} A^{k}=I+A+A^{2}+\cdots+A^{k}+\cdots\) 收敛的充要条件是 \(r(A)<1\),且收敛时,其和为 \((I-A)^{-1}\)
10.2 矩阵函数
幂级数:设幂级数 \(\sum_{k=0}^{\infty} c_{k} z^{k}\) 收敛半径为 \(r\),且当 \(|z|<r\) 时,幂级数收敛于函数 \(f(z)\),即 \(f(z)=\sum_{k=0}^{\infty} c_{k} z^{k}, \quad|z|<r\)
矩阵幂级数:如果 \(A\in C^{n\times n}\) 满足 \(r(A)<r\),则称收敛矩阵的矩阵幂级数 \(\sum_{k=0}^{\infty} a_{k} A^{k}\) 为矩阵函数,记为 \(f(A)\),即 \(f(A)=\sum_{k=0}^{\infty} c_{k} A^{k}\),考虑参数 \(t\),有 \(f(At)=\sum_{k=0}^{\infty} c_{k} (At)^{k}\)
- 常用矩阵函数:
- \(e^{A}=\sum_{k=0}^{\infty} \frac{1}{k !} A^{k}, \quad A \in C^{n \times n}\)
- \(\sin A=\sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2 k+1) !} A^{2 k+1}, \quad A \in C^{n \times n}\)
- \(\cos A=\sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2 k) !} A^{2 k}, \quad A \in C^{n \times n}\)
- \((E-A)^{-1}=\sum_{k=0}^{\infty} A^{k}, \quad r(A)<1\)
- \(\ln (E+A)=\sum_{k=0}^{\infty} \frac{(-1)^{k}}{k+1} A^{k+1}, \quad r(A)<1\)
矩阵函数值计算
相似对角化:设 \(P^{-1}AP=diag(\lambda_1,...,\lambda_n)=D\),则 \(f(At) = P\cdot diag(f(\lambda_1 t),...,f(\lambda_n t))\cdot P^{-1}\)
Jordan标准型:设 \(P^{-1}AP=diag(J_1,...,J_s)\),则 \[ f(A)=P\left(\begin{array}{ccc} {f\left(J_{1}\right)} & {} & {} \\ {} & {\ddots} & {} \\ {} & {} & {f\left(J_{s}\right)} \end{array}\right) P^{-1} \notag \]
矩阵函数性质
- 如果 \(AB=BA\),则
- \(e^{A} e^{B}=e^{B} e^{A}=e^{A+B}\)
- \(\cos (A+B)=\cos A \cos B-\sin A \sin B\)
- \(\sin (A+B)=\sin A \cos B+\cos A \sin B\)
- 如果 \(AB=BA\),则
11 矩阵求逆
Hermite矩阵的性质
- 一般 Hermite 矩阵
- Hermite 矩阵本身就是正规矩阵,因此可以对角化(几何重数等于代数重数),不同特征向量正交
- 特征值均为实数(反 Hermite 矩阵的特征值全为虚数)
- 正定 Hermite 矩阵
- 主对角线元素全部大于 0
- 存在正定 Hermite 矩阵 \(B\) 使得 \(A=B^2\)(可以无穷分解)
- \(A\) 的任意 k 行和对应的 k 列组成的主子阵是正定的