Particle Filter
今天我们来讲一下粒子滤波算法,这也是我在学习过程中的一个笔记,由于有很多的个人理解,有不对的地方欢迎大家批评指正。
[TOC]
1. 贝叶斯滤波
贝叶斯滤波是我们理解粒子滤波的基础。假设我们有如下图的隐马尔科夫模型(Hidden
Markov Model),并且有如下的系统方程与观测方程,我们只有观测值 \(\boldsymbol{y}_{1:T}\),但是现在想要根据观测值估计隐变量
\(\boldsymbol{x}_{1:T}\),也就是滤波所要做的事情。
\[
\begin{align}
\text{System Model}&: x_{k}=f_{k}\left(x_{k-1}, v_{k-1}\right) \\
\text{Observation Model}&: \mathrm{y}_{k}=h_{k}\left(\mathrm{x}_{k},
\mathrm{n}_{k}\right)
\end{align}
\]
假设我们现在已经处于 \(t_{k-1}\),且已经获得了 \(p({x}_{k-1}|\boldsymbol{y}_{1:k-1})\),这个概率分布的含义是什么呢?我们现在已经有了前 \(k-1\) 个时刻的观测值 \(\boldsymbol{y}_{1:k-1}\),并且根据这些观测值估计了 \(k-1\) 时刻隐变量 \(x_{k-1}\) 的后验概率分布,也即 \(p({x}_{k-1}|\boldsymbol{y}_{1:k-1})\)。那么接下来到 \(k\) 时刻,我们又获得了一个观测 \(y_k\),要怎么估计新的后验概率分布 \(p({x}_{k}|\boldsymbol{y}_{1:k})\) 呢?我们通过预测和更新两个阶段来估计,下面我就解释一下这两个阶段的含义。
1.1 预测
前面说了我们有系统模型和观测模型,首先根据系统模型,我们有了 \(k-1\) 时刻的后验,就可以根据 \(x_{k-1}\) 到 \(x_k\) 的转移模型得到 \(x_k\) 对应的概率分布,这个过程就叫做预测(Update)。通过预测阶段,我们可以获得先验概率分布(注意这里我们将 \(p({x}_k|\boldsymbol{y}_{1:k-1})\) 称为先验概率分布) \[ \begin{align}p({x}_k|\boldsymbol{y}_{1:k-1})=\int p({x}_k|x_{k-1})p(x_{k-1}|\boldsymbol{y}_{1:k-1})dx_{k-1}\end{align} \] 也就是说,我们即使没有观测值,也能对 \(x_k\) 的分布进行估计,但是由于没有利用观测值 \(y_k\) 带来的信息,因此这个估计是不准确的,下面我们就需要用观测值对这个先验概率分布进行纠正,也就是 更新阶段。
1.2 更新
有了先验,又有了观测,根据贝叶斯公式,我们可以很容易得到后验概率分布 \(p\left(x_{k} | \boldsymbol{y}_{1: k}\right)\)。怎么理解下面一个式子呢?我们有似然函数 \(p\left(y_{k} | x_{k}\right)\),现在有了观测 \(y_k\),那么似然值越大,表明对应的 \(x_k\) 的概率应该也越大, 就是用似然函数对先验概率进行加权就得到了后验概率。 \[ \begin{align} p\left(x_{k} | \boldsymbol{y}_{1: k}\right)&=\frac{p\left(y_{k} | x_{k},\boldsymbol{y}_{1: k-1}\right) p\left(x_{k} | \boldsymbol{y}_{1: k-1}\right)}{p\left(y_{k} | \boldsymbol{y}_{1: k-1}\right)} \\ &\propto p\left(y_{k} | x_{k},\boldsymbol{y}_{1: k-1}\right) p\left(x_{k} | \boldsymbol{y}_{1: k-1}\right) \\ &= p\left(y_{k} | x_{k}\right) p\left(x_{k} | \boldsymbol{y}_{1: k-1}\right) \end{align} \] > 怎么理解这个加权呢?举个栗子 > > 比如
总结
总结起来,我们滤波分为两个阶段 \[ \begin{align} \text{Prediction}&: p({x}_k|\boldsymbol{y}_{1:k-1})=\int p({x}_k|x_{k-1})p(x_{k-1}|\boldsymbol{y}_{1:k-1})dx_{k-1} \\ \text{Update}&: p\left(x_{k} | \boldsymbol{y}_{1: k}\right)\propto p\left(y_{k} | x_{k}\right) p\left(x_{k} | \boldsymbol{y}_{1: k-1}\right) \end{align} \] 可以看到,上面的预测阶段含有积分,这在实际当中往往是很难计算的,而对于那些非常规的PDF,甚至不能给出解析解。解决这种问题一般有两种思路:
- 建立简单的模型,获得解析解,如卡尔曼滤波(Kalman Filter)及EKF、UKF等;
- 建立复杂的模型,获得近似解,如粒子滤波(Particle Filter)等。
2. 卡尔曼滤波
卡尔曼滤波的思路就是将系统建模线性模型,隐变量、控制变量、控制噪声与观测噪声均为高斯分布,那么观测变量也是随机变量,整个模型中所有的随机变量都是高斯的!高斯分布是我们最喜欢的分布,因为在前面贝叶斯滤波的预测阶段我们可以不用积分了,只需要计算均值和协方差就可以了!根据系统模型和观测模型,我们可以获得滤波的闭式解,这就是卡尔曼滤波的思想。 \[ \begin{align} \text{System Model}&: \mathrm{x}_{k}=A\mathrm{x}_{k-1} + B\mathrm{u}_{k-1} + v_{k-1} \\ \text{Observation Model}&: \mathrm{y}_{k}=C\mathrm{x}_{k}+ \mathrm{n}_{k} \end{align} \] 但实际中要求线性系统模型往往是很困难的,对于非线性模型,如果我们还想应用卡尔曼滤波该怎么办呢?线性近似,也就是求一个雅可比矩阵(Jacobi),这就是扩展卡尔曼滤波(EKF)。
3. 大数定律
粒子滤波是什么是意思呢?我们可以用大量的采样值来描述一个概率分布,当我们按照一个概率分布进行采样的时候,某个点的概率密度越高,这个点被采到的概率越大,当采样数目足够大(趋于无穷)的时候,粒子出现的频率就可以用来表示对应的分布,实际中我们可以理解一个粒子就是一个采样。

但是对于离散型的随机变量还好,可以很容易的求出来状态空间中每个状态的频率。但如果对于连续分布,其实是很不方便的,所幸实际中我们也不需要获得概率分布的全部信息,一般只需要求出期望就可以了。
下面为了公式书写和推导方便,以离散型随机变量为例,假设状态空间为 \(\mathcal{Z}=\{1,2,...,K\}\),有 \(N\) 个采样样本 \(z_i \in \mathcal{Z}\),服从概率分布 \(q(\mathbf{z})\)。我们将根据 \(N\) 个采样样本 \(\boldsymbol{z}_{1:N}\) 得到的分布记为经验分布 \(\hat{p}(b|\boldsymbol{z}_{1:N}) = \frac{1}{N}\sum_i \mathbb{I}(b-z_i)\),其中 \(\mathbb{I}(\cdot)\) 为指示函数,那么当 \(N\) 足够大的时候,经验分布 \(\hat{p}(b|\boldsymbol{z}_{1:N})\) 就足够接近真实分布 \(q(\mathbf{z})\)。现在我们想估计随机变量 \(\mathsf{t}=g(\mathsf{z})\) 的期望,即 \[ \begin{align} \mathbb{E}[\mathsf{t}] &= \mathbb{E}[g(\mathsf{z})]=\sum_{b\in\mathcal{Z}}g(b)q(b) \notag\\ &\approx \sum_b g(b)\hat{p}(b|\boldsymbol{z}_{1:N}) \notag\\ &= \sum_b g(b)\frac{1}{N}\sum_i \mathbb{I}(b-z_i) \notag\\ &= \frac{1}{N}\sum_i g(z_i) \end{align} \] 也就是说,我们只需要对样本进行简单求和就可以了!连续型随机变量也是类似的,所以在后面的粒子滤波中,我们利用粒子估计了概率密度分布,要想求期望就只需要进行求和平均就可以了。
4. 粒子滤波简单实例
好了,有了前面的预备知识,我们可以先看一个粒子滤波的简单例子。
假设我们现在有采样好的 \(N\) 个粒子 \(\{x_{k-1}^i\}_{i=1}^N\),他们服从分布 \(p({x}_{k-1}|\boldsymbol{y}_{1:k-1})\),那么我们现在如何进行贝叶斯滤波中的预测和更新阶段呢?
4.1 预测
回顾一下预测的公式 \[ \text{Prediction}: p({x}_k|\boldsymbol{y}_{1:k-1})=\int p({x}_k|x_{k-1})p(x_{k-1}|\boldsymbol{y}_{1:k-1})dx_{k-1} \\ \] 想一下:只要我们让每个粒子 \(x_{k-1}^i\) “进化”一步,也就是说按照分布 \(p(x_k|x_{k-1})\) 进行采样,使得 \(x_k^i \sim p(x_k|x_{k-1}^i)\),这样我们就获得了 \(N\) 个新的粒子 \(\{x_k^i\}_{i=1}^N\)。很容易验证,如果 \(\{x_{k-1}^i\}_{i=1}^N\) 能够很好的表示 \(p({x}_{k-1}|\boldsymbol{y}_{1:k-1})\) 的话,那么 \(\{x_k^i\}_{i=1}^N\) 也能很好的表示 \(p({x}_k|\boldsymbol{y}_{1:k-1})\)(这一部分可以凭直观感觉来理解,这是一个很自然的事情,也可以用前面的经验分布的思路进行公式推导)。
这样做的好处是什么呢?我们避免了积分!只需要对一个已知的分布 \(p(x_k|x_{k-1}^i)\) 进行采样,而这个分布是我们假设的系统模型,可以是很简单的,因此采样也很方便。
4.2 更新
通过预测我们获得了 \(x_k^i \sim p(x_k|x_{k-1}^i)\),这 \(N\) 个粒子就描述了先验概率分布。接下来就是更新,再回顾一下更新的公式 \[ \text{Update}: p\left(x_{k} | \boldsymbol{y}_{1: k}\right)\propto p\left(y_{k} | x_{k}\right) p\left(x_{k} | \boldsymbol{y}_{1: k-1}\right) \] 更新是什么呢?前面提到了:更新就是用似然函数对先验概率进行加权就得到了后验概率。如果简单的把 \(x_k^i\) 带入到上面的公式里,就可以得到下面的式子 \[ p\left(x_{k}^i | \boldsymbol{y}_{1: k}\right)\propto p\left(y_{k} | x_{k}^i\right) p\left(x_{k}^i | \boldsymbol{y}_{1: k-1}\right) \] 实际上就表示每个粒子有不同的权重。
这里怎么理解呢?想一下前面提到的经验分布,我们只需要用粒子出现的频率来表示对应的概率,实际上就是在统计频率的时候每个粒子的权重都是相同的,出现一次计数就加一。
而这里的区别是什么呢?由于我们有一个观测值 \(y_k\),根据 \(y_k\) 来反推,某一个粒子 \(i_1\) 的导致 \(y_k\) 出现的概率更大,那么我们在统计频率的时候,就给这个粒子加一个更大的权重,以表示我们更相信/重视这个粒子。
那么问题来了,前面我们说了滤波过程中要想求期望,只需要简单求和就可以了 \[ \mathbb{E}[\mathsf{t}] = \frac{1}{N}\sum_i g(z_i) \] 现在粒子有了权重怎么办呢,同理,加个权就好了(推导也很简单,相信大家都会),下面的式子里对权重进行了归一化 \[ \mathbb{E}[\mathsf{t}] = \sum_i \frac{w_i}{\sum_j w_j}g(z_i) \]
4.3 递推
前面只讲了一次预测和一次更新的过程,注意到我们前面只是从 \(k-1\) 到 \(k\) 时刻的滤波过程,但每一轮循环原理都是相同的。
不过细心的朋友们可能会觉得不太对劲,前面一个阶段的例子里,预测之前我们有采样 \(\{x_{k-1}^i\}_{i=1}^N\),推导过程中我们是默认这些粒子的权重都是相同的,然后我们进行了预测和更新,但是更新之后我们给每个粒子加权了呀,到下一个阶段怎么办?!!!也很简单,预测阶段不必要求每个粒子的权重都相同,也加上一个权重就好了。也就是说我们时时刻刻都保存有每个粒子的权重信息。
这样我们就可以得到一个完整的粒子滤波算法了!但是还有问题!
重采样
但是呢,有人发现了上面的算法不好啊!不是因为麻烦,而是滤波到最后会发现只有少数一部分粒子有很大的权重,而其他绝大部分粒子的权重几乎为 0,这就意味着对于那些“不重要”的粒子,他们在我们求期望的时候贡献并不大,但是我们却花费了大量的计算精力来维护这些粒子,这样不好不好!于是就有人提出了重采样。
重采样什么意思呢?你们粒子的权重不是不同吗,那我就采取手段给你们整相同了!简单理解,有两个粒子,粒子 \(a\) 的权重是 8,粒子 \(b\) 权重是 2,那我就把粒子 \(a\) 复制 8 份,粒子 \(b\) 复制 2 份,这样得到的 10 个粒子权重就都是 1 了。但是另一个问题是一开始我们只有 2 个粒子,这样弄完我们就有 10 个粒子了,如果一直这么做我们的粒子数会越来越多,算力跟不上。那就从这 10 个粒子里均匀分布地随机抽 2 个!那么粒子 \(a\) 的概率就是 \(0.8\),这就成了。
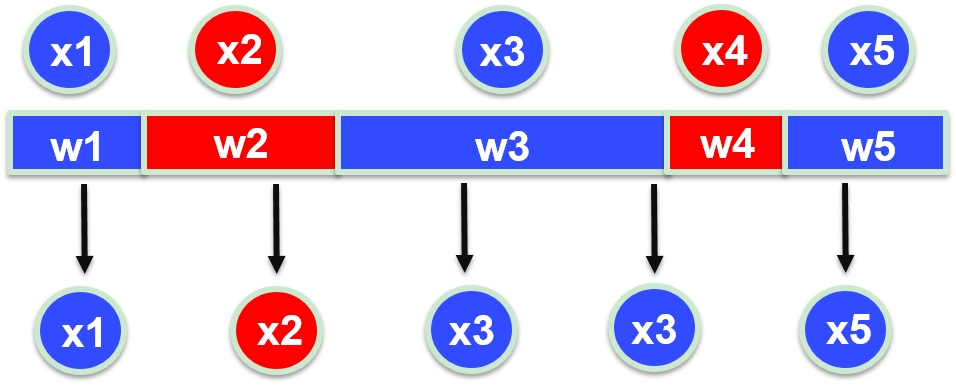
至此,加上重采样我们就获得了一个完整的比较好用的粒子滤波算法

5. 粒子滤波原理推导
但是还有一个问题,就是前面我们直接说有 \(N\) 个粒子 \(x_{k-1}^i \sim p({x}_{k-1}|\boldsymbol{y}_{1:k-1})\),但是第 1 步(刚开始)的时候我们怎么获得这些粒子来描述 \(p(x_1|y_1)\) 啊?如果是高斯分布还好,我们可以很方便的对高斯分布进行采样,但是如果是一个特别特别特别复杂的分布呢?我们甚至不能写出解析表达式,更没办法按照这个分布进行随机采样,那我们是不是就凉了?不!我们前面不是讲了粒子可以有权重嘛。
假如我们现在有另一个分布 \(q(\mathbf{x}_{1:k}|\mathbf{y}_{1:k})\),这个分布是我们自己指定的,可以很简单,而且我们可以按照这个分布来进行采样,那么我们就有 \(x_{k-1}^i \sim q(\mathbf{x}_{1:k}|\mathbf{y}_{1:k})\),那么我们怎么用这些粒子来表示我们想要得到的真正的分布 \(p(\mathbf{x}_{0:k}|\mathbf{y}_{1:k})\) 呢?再加个权就行了,就像前面用似然函数进行加权。 \[ \begin{align} p(\mathbf{x}_{0:k}|\mathbf{y}_{1:k})&\approx \sum_{i=1}^{N}w_k^i\delta(\mathbf{x}_{0:k}-\mathbf{x}_{0:k}^i) \notag \\ w_{k}^{i} &\propto \frac{p\left(\mathbf{x}_{0: k}^{i} | \mathbf{y}_{1: k}\right)}{q\left(\mathbf{x}_{0: k}^{i} | \mathbf{y}_{1: k}\right)} \notag\end{align} \] 再考虑前面提到的的预测和更新两个递推进行的阶段,就有 \[ \begin{align}q\left(\mathbf{x}_{0: k} | \mathbf{y}_{1: k}\right)&=q\left(\mathbf{x}_{k} | \mathbf{x}_{0: k-1}, \mathbf{y}_{1: k}\right) q\left(\mathbf{x}_{0: k-1} | \mathbf{y}_{1: k-1}\right) \notag\\ &= q\left(\mathbf{x}_{k} | \mathbf{x}_{k-1}, \mathbf{y}_{ k}\right) q\left(\mathbf{x}_{0: k-1} | \mathbf{y}_{1: k-1}\right) \notag \\ w_{k}^{i} &\propto w_{k-1}^{i} \frac{p\left(\mathbf{y}_{k} | \mathbf{x}_{k}^{i}\right) p\left(\mathbf{x}_{k}^{i} | \mathbf{x}_{k-1}^{i}\right)}{q\left(\mathbf{x}_{k}^{i} | \mathbf{x}_{k-1}^{i}, \mathbf{y}_{k}\right)} \label{eq_sis} \end{align} \] 然后我们就得到了一个更加 universal/generic 的粒子滤波算法(下面图片所示算法中没加重采样步骤)。

6. 总结
这篇文章主要是自己学习粒子滤波之后的一些理解,主要参考了文章 A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking,但是这篇文章中是从 general 的情况开始讲,然后举了一些常用的特例,个人感觉不利于初学者理解,因此本文写作过程中的思路是从简单的特例开始再到更一般的情况。
最后一部分 粒子滤波原理推导 其实写的并没有很清楚,主要是因为自己太懒,到最后懒得一个个手敲公式了,如果想更清楚地了解其中的细节,可以阅读上面那篇论文。
7. Reference
- M. S. Arulampalam, S. Maskell, N. Gordon and T. Clapp, "A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking," in IEEE Transactions on Signal Processing, vol. 50, no. 2, pp. 174-188, Feb. 2002.